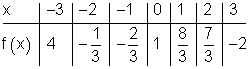Bei diesen Mathematik Aufgaben zu ganzrationalen Funktionen aus gegebenen Bedingungen I sollst du Wertetabellen aufstellen und Graphen zeichnen etc. Viel Erfolg!
1. Gegeben ist die Wertetabelle einer ganzrationalen Funktion 3. Grades
Skizziere den Graphen und mache eine Aussage über die Funktion.
2. Eine ganzrationale Funktion 3. Ordnung verläuft durch die gegebenen Punkte
Bestimme die Funktionsgleichung und die Achsenschnittpunkte. Stelle eine Wertetabelle auf und zeichne den Graphen.
a)
![]()
b)
![]()
Um die Funktionsgleichung zu bekommen, kannst du dir das 📽️Video Gauss-Algorithmus 3 Gleichungen mit 3 Variablen lösen ansehen.
Außerdem kannst du dir das 📽️ Video Horner-Schema: Funktionswerte berechnen ansehen.
3. Bestimme den zugehörigen Funktionsterm
Eine zur y-Achse symmetrische ganzrationale Funktion 4. Grades verläuft durch die gegebenen Punkte. Bestimme den zugehörigen Funktionsterm.
a)
![]()
b)
![]()
c)
![]()
d)
![]()
4. Bestimme jeweils die Funktionsgleichung
Eine ganzrationale Funktion 4. Grades verläuft durch folgende Punkte.
a)
![]()
b)
![]()
c)
Der Graph einer ganzrationalen Funktion 4. Grades hat in P1 einen Sattelpunkt, schneidet die x-Achse in Px und verläuft durch den Punkt P2. Bestimme den Funktionsterm.
6. Bestimme die Funktionsgleichung f(x)
Der Graph einer ganzrationalen Funktion 4. Grades ist achsensymmetrisch und schneidet die y- Achse in Py . Weiterhin verläuft er durch die Punkte P1 und P2. Bestimme die Funktionsgleichung f(x). Wie erhält man g(x) aus f(x)?
7. Bestimme einen möglichen Funktionsterm
Der Graph der Funktion f(x) schneidet eine Parallele zur x- Achse im Abstand 3 in x = 0 und x = 2. x = 0 ist dreifache Schnittstelle.
8. Zeige und zeichne
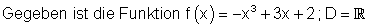
a)
![]()
b)
![]()
Dazu findest du hier die ausführlichen Lösungen.
Und hier die Aufgaben Ganzrationale Funktionen gegebene Bedingungen IV.
Die Aufgaben Ganzrationale Funktionen aus gegebenen Bedingungen II und III sind in den Materialien enthalten, die Sie hier erwerben können.
Die Theorie findest du hier: Aufstellen der Funktionsgleichung aus gegebenen Bedingungen.
Hier eine Übersicht über alle Beiträge zur weiteren ganzrationalen Funktionen.