Hier findest du die Lösungen zu den Aufgaben VK I, also zur Vorbereitung einer Klassenarbeit Teil I, in denen du die Funktionsgleichungen von Geraden und Parabeln bestimmen sollst.
1. Eine Gerade mit der Steigung a = -4/5
verläuft durch den Punkt P1 ( 3 | -2 ).
Ermittele die Funktionsgleichung f(x) und zeichne die Gerade in ein Koordinatensystem!
Ausführliche Lösung
Als erstes stellen wir den Ansatz auf:
f(x) = a_1x + a_0 mit a_1 = -\frac{4}{5} wird
f(x) = -\frac{4}{5}x + a_0
Die Punktrobe mit P_1 (3 | -2) ergibt: \\
f(3) = -2 \Leftrightarrow -\frac{4}{5} \cdot 3 + a_0 = - 2 | +\frac{12}{5} \\
\Leftrightarrow a_0 = \frac{2}{5} \\
\underline{\underline{f(x) = -\frac{4}{5}x + \frac{2}{5} }}
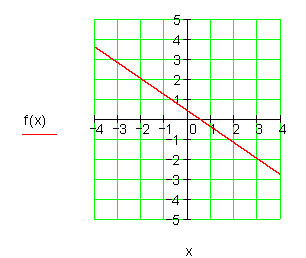
2. Gegeben sind die Punkte P1 und P2
die auf einer Geraden liegen. Ermittele die Funktionsgleichung f(x) und zeichne den Graphen!
P_1(-4 | 1,5) ; P_2(3,5 | -3)
Ausführliche Lösung:
f(x) = a_1x + a_0
P_1 (-4 | \frac{3}{2} ; P_2 (\frac{7}{2} | -3) \\
a_1 = \dfrac{y_2 -y_1}{x_2 - x_1} = \dfrac{-3 - \frac{3}{2} }{ \frac{7}{2} - (-4)} = -\frac{3}{5} \\
\Rightarrow f(x) = -\frac{3}{5}x + a_0
Punktprobe mit P_1 (-4 | \frac{3}{2}) ergibt:
f(-4) = \frac{3}{2} \\
\Leftrightarrow -\frac{3}{5} \cdot (-4) + a_0 = \frac{3}{2} | - \frac{12}{5} \\
\Leftrightarrow a_0 = -\frac{9}{10} \\
\underline{\underline{f(x) = -\frac{3}{5} x - -\frac{9}{10} }}
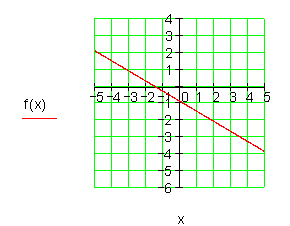
3. Bestimme den Schnittpunkt
der beiden Geraden mit den Funktionsgleichungen f(x) = x + 2 und g(x) = -x +4
Zeichne beide Geraden in ein Koordinatensystem!
Ausführliche Lösung
P(x_s | y_s) sei der Schnittpunkt beider Geraden.
Als erstes erstellen wir wieder den Ansatz und setzen beide Funktionsgleichungen gleich:
f(x) = g(x)
x_s + 2 = -x_s +4 | + x_s \\
\Leftrightarrow 2x_s + 2 = 4 | -2 \\ \Leftrightarrow 2x_s = 2 | : 2 \\
\Leftrightarrow x_s = 1
Dies ist also die x-Koordinate des Schnittpunktes.
y_s = f(x_s) = f(1) = 1 + 2 = 3 \Rightarrow \underline{\underline{ P(1 | 3)}} ist der Geradenschnittpunkt.
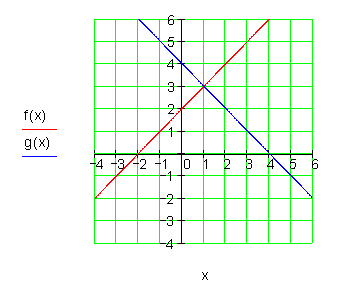
4. a) Berechne die Scheitelpunktform und den Scheitelpunkt!
Zeichne die Parabeln!
Ausführliche Lösung
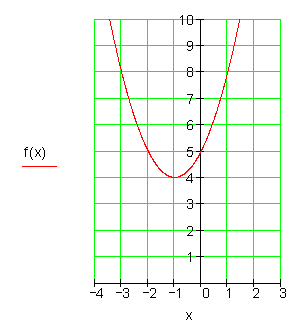
f(x) = x^2 + 2x + 5 Zum Lösen benutzen wir die quadratische Ergänzung.
f(x) = \color{red}{ x^2 + 2x + 1^2} - 1^2 + 5 Dadurch erhalten wir in dem roten Teil die erste binomische Formel. f(x) = (x + 1)^2 +4
Dies ist die Scheitelpunktform. S(-1 | 4} ist der Scheitelpunkt.
4. b)
Berechne die Scheitelpunktform und den Scheitelpunkt! Zeichne die Parabeln!
Ausführliche Lösung
f(x) = \frac{1}{2}x^2 -x - \frac{17}{2} Jetzt können wir den Faktor \frac{1}{2} ausklammern und wieder quadratisch ergänzen:
f(x) = \frac{1}{2}[x^2 - 2x - 17] \\
\Leftrightarrow f(x) = \frac{1}{2}[\color{red}{x^2 - 2x + 1^2} \color{black}{- 1^2 - 17}]
In dem rot markierten Teil können wir jetzt die zweite binomische Formel erkennen.
\Leftrightarrow f(x) = \frac{1}{2}[(x - 1)^2 - 18] \\
\Rightarrow \color{red}{f(x) = \frac{1}{2}(x - 1)^2 - 9 \Rightarrow S(1 | -9)}
5. Beschreibe schrittweise,
wie f(x) aus der Normalparabel entsteht und wie sie geöffnet ist. Welche Koordinaten hat der Scheitelpunkt?
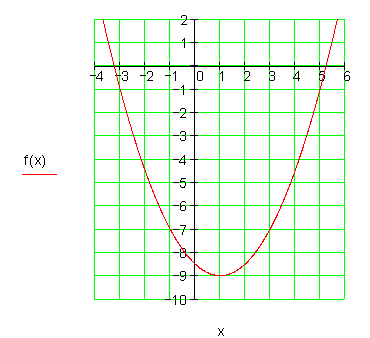
5. a) f(x) = (x + 2)^2 -9
b) f(x) = 0,5 (x - 4)^2 - 3
c) f(x) = -\frac{7}{3} (x - \frac{3}{2})^2 + \frac{5}{4}
d) f(x) = -4 (x + \frac{3}{4})^2 - \frac{1}{3}
Ausführliche Lösung
a) Normalparabel verschoben um 2 EH nach links, um 9 EH nach unten, nach oben geöffnet.Der Scheitelpunkt hat die Koordinaten: S(-2 | -9)
b) Normalparabel verschoben um 4 EH nach rechts, um 3 EH nach unten, nach oben geöffnet, um den Faktor1/2 gestaucht. Der Scheitelpunkt hat die Koordinaten: S(4 | -3)
c) Normalparabel verschoben um 3/2 EH nach rechts, um 5/4 EH nach oben, nach unten geöffnet, um den Faktor 7/3 gestreckt. Der Scheitelpunkt hat die Koordinaten: s(\frac{3}{2} | \frac{5}{4})
d) Normalparabel verschoben um 3/4 EH nach links, um 1/3 EH nach unten, nach unten geöffnet, um den Faktor 4 gestreckt. Der Scheitelpunkt hat die Koordinaten. S(-\frac{3}{4} | -\frac{1}{3})
6. Eine Normalparabel
wird mit dem Formfaktor -0,4 gestaucht und um 4 Einheiten nach rechts und um 3 Einheiten nach unten verschoben. Bestimme die Funktionsgleichung. Wie ist die Parabel geöffnet?
Ausführliche Lösung
f(x) = -\frac{2}{5} (x - 4)^2 - 3
Dabei ist -\frac{2}{5} der Formfaktor, durch – 4 wird die Parabel nach rechts verschoben und durch -3 nach unten. Die Parabel ist nach unten geöffnet, weil der Formfaktor negativ ist.
7. a) Berechne die Achsenschnittpunkte und zeichne folgende Parabel!
Ausführliche Lösung
f(x) = (x + 2)^2 - 9
Als erstes erstellen wir den Ansatz für die Nullstellen:
f(x) = 0 \Leftrightarrow (x + 2)^2 - 9 = 0 | + 9 \\
\Leftrightarrow (x + 2)^2 = 9 | √ \\
\Leftrightarrow | x + 2 | = 3
Daraus ergibt sich 1. x + 2 = 3 \Rightarrow x_1 = 1 \\ 2. x + 2 = -3 \Rightarrow x_2 = -5
Somit ist der Ansatz für P_y : y_s = f(0) = (0 + 2)^2 - 9 = -5
Die Achsenschnittpunkte sind folglich: \color{red}{P_{x1} (1 | 0) ; P_{x2} (-5 |0) ; P_y (0 | -5)}
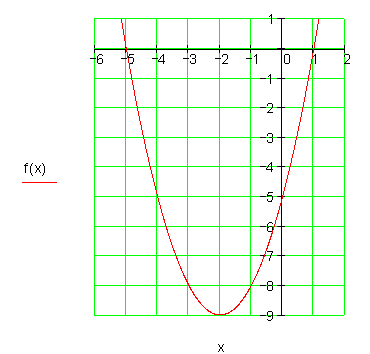
7. b)
Berechne die Achsenschnittpunkte und zeichne folgende Parabel.
Ausführliche Lösung:
f(x) = -(x + 2)^2 + 5
Als erstes erstellen wir den Ansatz für die Nullstellen:
f(x) = 0 \Leftrightarrow -(x + 2)^2 + 5 = 0 | -5 \\
\Leftrightarrow -(x + 2)^2 = 5 | √ \\
\Leftrightarrow | x + 2 | = \sqrt 5
Daraus ergibt sich 1. x + 2 = \sqrt 5 \Rightarrow x_1 = -2 + \sqrt 5 \approx 0,24 \\ 2. x + 2 = -\sqrt 5 \Rightarrow x_2 = -2 - \sqrt 5 \approx -4,24
Somit ist der Ansatz für P_y : y_s = f(0) = -(0 + 2)^2 + 5 = 1
Die Achsenschnittpunkte sind folglich: \color{red}{P_{x1} (-2 + \sqrt 5 \approx 0,24 | 0) ; P_{x2} (-2 - \sqrt 5 \approx -4,24 |0) ; P_y (0 | 1)}
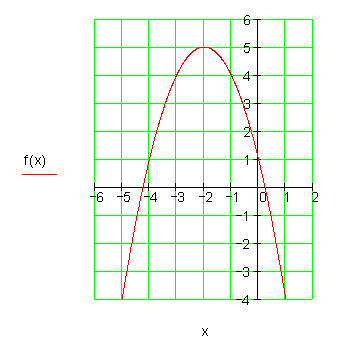
7. c)
Berechne die Achsenschnittpunkte und zeichne folgende Parabel.
Ausführliche Lösung
f(x) = -x^2 + x + 6
Als erstes erstellen wir den Ansatz für die Nullstellen:
f(x) = 0 \Leftrightarrow -x^2 + x + 6 = 0 | \cdot (-1) \\
\Leftrightarrow x^2 - x - 6 = 0
Nachdem wir + (\frac{1}{2})^2 - (\frac{1}{2})^2 ergänzt haben, erkennen wir in dem rot markierten Bereich die 2. binomische Formel.
\Leftrightarrow \color{red}{x^2 - x + (\frac{1}{2})^2} - (\frac{1}{2})^2 - 6 = 0
Und da -(\frac{1}{2})^2 - 6 = -\frac{25}{4} :
\Leftrightarrow (x - \frac{1}{2})^2 - \frac{25}{4} = 0 | + \frac{25}{4} \\ \Leftrightarrow
(x - \frac{1}{2})^2 = \frac{25}{4} |√ \\
\Leftrightarrow | x - \frac{1}{2} | = \frac{5}{2}
Daraus ergibt sich 1. x - \frac{1}{2} = \frac{5}{2} \Rightarrow x_1 = 3 \\ 2. x - \frac{1}{2} = -\frac{5}{2} \Rightarrow x_2 = -2
Somit ist der Ansatz für P_y : y_s = f(0) = 0^2+ 0 + 6 = 6
Die Achsenschnittpunkte sind folglich: \color{red}{P_{x1} (3 | 0) ; P_{x2} (-2 |0) ; P_y (0 | 6)}
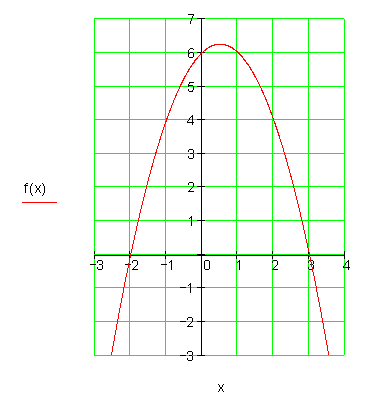
7. d)
Berechne die Achsenschnittpunkte und zeichne folgende Parabel.
Ausführliche Lösung
f(x) = -\frac{1}{2}x^2 - 2x + 6
Wir erstellen wieder den Ansatz für die Nullstellen:
f(x) = 0 \Leftrightarrow -\frac{1}{2}x^2 - 2x + 6 = 0 | : (-\frac{1}{2}) \\
\Leftrightarrow x^2 + 4x - 12 = 0
Nachdem wir + (2)^2 - (2)^2 ergänzt haben, erkennen wir in dem rot markierten Bereich die 1. binomische Formel.
\Leftrightarrow \color{red}{x^2 + 4x + (2)^2} - (2)^2 -12 = 0
\Leftrightarrow (x + 2)^2 - 16 = 0 | + 16
\\ \Leftrightarrow (x +2)^2 = 16 | √ \\ \Leftrightarrow | x +2 | = 4
Daraus ergibt sich 1. x +2 = 4 \Rightarrow x_1 = 4 \\ 2. x + 2 = -4 \Rightarrow x_2 = -6
Somit ist der Ansatz für P_y : y_s = f(0) = -\frac{1}{2} \cdot 0^2 - 2 \cdot 0 + 6 = 6
Die Achsenschnittpunkte sind folglich: \color{red}{P_{x1} (2 | 0) ; P_{x2} (-6 |0) ; P_y (0 | 6)}
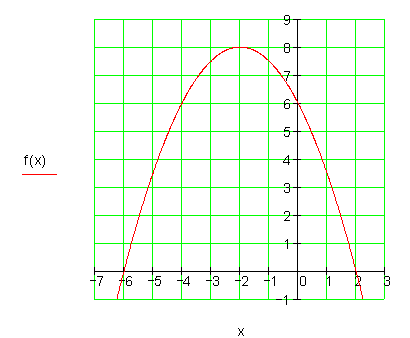
8. a) Berechne die Scheitelpunktform und den Scheitelpunkt.
Zeichne die Parabel.
f(x) = -x^2 + x + 6
Die Nullstellen sind bei x_1 = -2 und x_2 = 3
Ausführliche Lösung
f(x) = -x^2 + x + 6 Scheitelpunkt über Nullstellen
x_s = \dfrac{x_1 + x_2}{2} = \frac{-2 + 3 }{2} = \frac{1}{2} \\
y_s = f(x_s) = f(\frac{1}{2}) = -(\frac{1}{2})^2 + \frac{1}{2} + 6 =\frac{25}{4} \\ \color{red}{S(\frac{1}{2} = 0,5 | \frac{25}{4} = 6,25) f(x) = (x - \frac{1}{2})^2 + \frac{25}{4} }
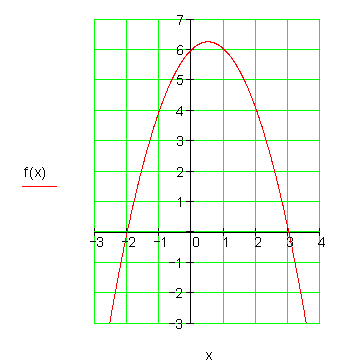
8. b)
Berechne die Scheitelpunktform und den Scheitelpunkt. Zeichne die Parabel.
f(x) = x^2 + 6x + 4
Die Nullstellen sind bei x_1 = -3 + \sqrt 5 und x_2 = -3 - \sqrt 5
Ausführliche Lösung
f(x) =x^2 + 6x + 4 Scheitelpunkt über Nullstellen
x_s = \dfrac{x_1 + x_2}{2} = \dfrac{-3 + \sqrt 5 + ( -3 - \sqrt 5)}{2} = -3 \\
y_s = f(x_s) = f(-3) = (-3)^2 + 6 \cdot (-3) + 4 = -5 \\
\color{red}{S(-3 | -5) f(x) = (x + 3)^2 - 5 }
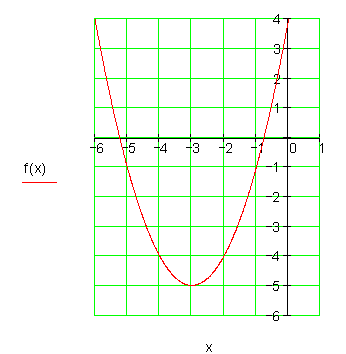
9. Bestimme die Schnittpunkte von Parabel und Gerade.
Ausführliche Lösung
f(x) = x^2 + 5x + \frac{9}{4} g(x) = -\frac{3}{2}x - 5\frac{1}{4}
Als erstes stellen wir den Ansatz auf:
f(x) = g(x) \Leftrightarrow x^2 + 5x + \frac{9}{4} = -\frac{3}{2}x - 5\frac{1}{4} | + \frac{3}{2}x \\
\Leftrightarrow x^2 + \frac{13}{2}x + \frac{9}{4} = -\frac{21}{4} | + \frac{21}{4} \\
\Leftrightarrow x^2 + \frac{13}{2}x + \frac{15}{2} = 0
Dies lösen wir durch quadratische Ergänzung indem wir (\frac{13}{4})^2 - (\frac{13}{4})^2 ergänzen:
\Leftrightarrow x^2 + \frac{13}{2}x + \color{red}{ (\frac{13}{4})^2 } - (\frac{13}{4})^2 + \frac{15}{2} = 0 \\
\Leftrightarrow (x + \frac{13}{4})^2 - \frac{49}{16} = 0
| + \frac{49}{16} \\ \Leftrightarrow (x + \frac{13}{4})^2 = \frac{49}{16} | √ \\
\Leftrightarrow | x + \frac{13}{4} | = \frac{7}{4}
Fall 1 : x + \frac{13}{4} = \frac{7}{4} \Rightarrow x_1 = -\frac{3}{2}
Fall 2: x + \frac{13}{4} = -\frac{7}{4} \Rightarrow x_2 = -5
Die Schnittpunkte:
x_1 und x_2 sind die x-Koordinaten der Schnittpunkte. Die y-Koordinaten der Schnittpunkte finden wir, indem wir in f(x) oder in g(x) einsetzen.
y_1 = g(x_1) = g(-\frac{3}{2}) = -\frac{3}{2} \cdot (-\frac{3}{2}) - \frac{21}{4} = -3
y_2 = g(x_2) = g(-5) = -\frac{3}{2} \cdot (-5) - \frac{21}{4} = \frac{9}{4}
Die Gerade schneidet die Parabel also in den Punkte P_1(-\frac{3}{2} | -3) und P_2(-5 | \frac{9}{4})
10. Gegeben sind die Funktionsgleichungen zweier Parabeln,
von denen die Schnittpunkte zu bestimmen sind.
Ausführliche Lösung
f(x) = x^2 - 4x + 1 und g(x) = -x^2 + 2x + 1
Als erstes stellen wir den Ansatz auf:
f(x) = g(x) \Leftrightarrow x^2 - 4x + 1 = -x^2 + 2x + 1 | + x^2 \\
\Leftrightarrow 2x^2 -4x + 1 = 2x +1 | -2 \\
\Leftrightarrow 2x^2 - 6x +1 = 1 | -1 \\ \Leftrightarrow 2x^2 - 6x = 0 | : 2 \\ \Leftrightarrow x^2 - 3x = 0
Wir nutzen wieder die quadratische Ergänzung und setzen danach die 2. binomische Formel ein:
\Leftrightarrow x^2 - 3x \color{red}{+ (\frac{3}{2})^2 - (\frac{3}{2})^2 } = 0 \\
\Leftrightarrow (x - \frac{3}{2})^2 = \frac{9}{4}
| √ \Leftrightarrow |x - \frac{3}{2} | = \frac{3}{2}
Fall 1.: x - \frac{3}{2} = \frac{3}{2} \Rightarrow x_1 = 3
Fall 2.: x - \frac{3}{2} = - \frac{3}{2} \Rightarrow x_2 = 0 \\
y_1 = f(x_1) = f(3) = 3^2 - 4 \cdot 3 + 1 = - 2 \\
y_2 = f(x_2) = f(0) = 0^2 - 4 \cdot 0 + 1 = 1
Die Parabeln schneiden sich in den Punkten P_1(3 | -2) und P_2(0 | 1)
11. Berechne die Funktionsgleichung h(x)
der Verbindungsgeraden der Scheitelpunkte folgender Parabeln:
Ausführliche Lösung
f(x) = \frac{1}{2}(x - 4)^2 - 3 \Rightarrow S_1(4 | - 3) \\
g(x) = \frac{2}{3}(x + 3)^2 - 6 \Rightarrow S_2(-3 | -6)
Die Gerade verläuft durch die beiden Scheitelpunkte.
Ansatz:
f_g(x) = a_1x + a_0 \\
a_1 = \dfrac{y_2 - y_1}{x_2 - x_1} = \frac{-6 - (-3)}{-3 - 4} = \frac{3}{7}
f_g(x) = \frac{3}{7}x + a_0
Punktprobe mit S_1(4 | -3): \\
f_g(4) = 3 \Leftrightarrow \frac{3}{7} \cdot 4 + a_0 = -3 | -\frac{3}{7} \\
\Leftrightarrow a_0 = -\frac{33}{7} \Rightarrow \color{red}{ f_g(x) = \frac{3}{7}x - \frac{33}{7}}
12. Bestimme den Abstand der Scheitelpunkte beider Parabeln voneinander.
![]()
Ausführliche Lösung
Da beide Scheitelpunkte die x- Koordinate x = -2 haben, liegen sie übereinander. Der Abstand berechnet sich aus dem Betrag der Differenz der y- Koordinaten. Er beträgt 7 EH.
![]()
Hier findest du die Aufgaben
hier die dazugehörige Theorie: Zusammenfassung Quadratische Funktionen
und hier eine Übersicht über weitere Beiträge zu quadratische Funktionen, darin auch Links zu weiteren Aufgaben.

