Hier findest du die Lösungen der Aufgaben zu linearen Gleichungen mit Sachaufgaben, Textaufgaben und komplettem Lösungsweg. Z. B.: drei Geschwister sind zusammen 21 Jahre alt.
Dazu können dir diese Videos helfen: Playlist aller Videos zu linearen Gleichungen .
1. Bestimme die Definitions- und Lösungsmenge!
Ausführliche Lösungen:
a)
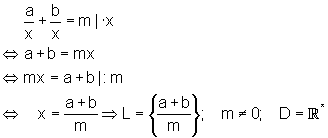
b)
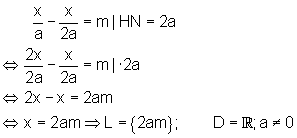
c)
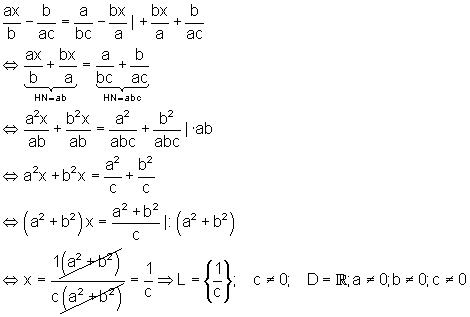
d)
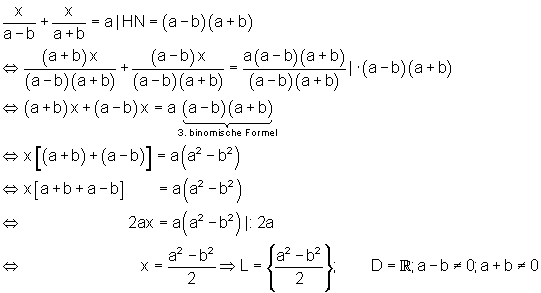
2. Bestimme die Definitions- und Lösungsmenge!
Ausführliche Lösungen:
a)
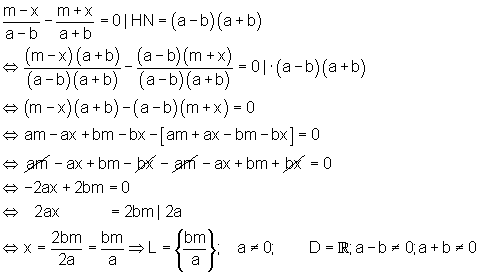
b)
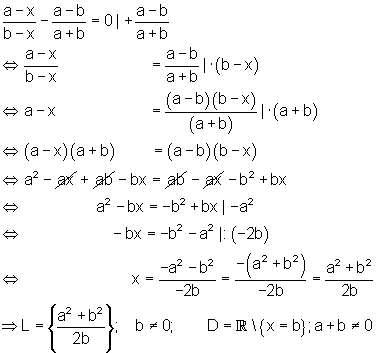
c)
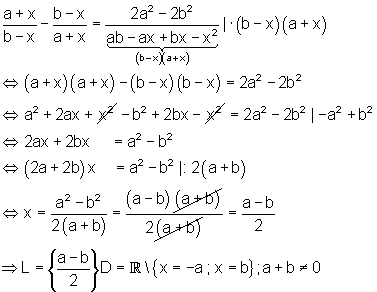
d)
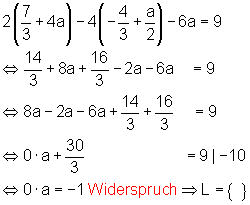
Somit gibt es keine Lösung.
3. Drei Geschwister sind zusammen 21 Jahre alt.
A ist doppelt so alt wie B und C ist nur halb so alt wie B. Wie alt ist jedes der Geschwister?
Ausführliche Lösung:
Ansatz:
Drei Geschwister sind zusammen 21 Jahre alt:
1. A + B + C = 21 (1)
2. A ist doppelt so alt wie B:
3. A = 2B (2)
4. C ist nur halb so alt wie B:
5. C = B/2 (3)
Damit ist die Unbekannte die Variable B.
Aus Gleichung (1) wird nun:
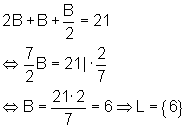
Aus (2) und (3) ergibt sich somit:
A = 2B = 12. B = 6 wurde berechnet. C = B/2 = 3
Die Geschwister sind 12, 6 und 3 Jahre alt.
In diesem 
4. Ein Behälter kann durch zwei Zuflussröhren gefüllt werden.
Die erste füllt ihn in 10 min und die zweite in 15 min. In wie viel Minuten wird er gefüllt, wenn beide Röhren gleichzeitig in Betrieb sind?
Ausführliche Lösung:
Ansatz:
Das erste Rohr füllt den Behälter in einer Minute 1/10.
Das zweite Rohr füllt den Behälter in einer Minute 1/15.
Gesucht ist die Zeit in Minuten, also die Variable x.
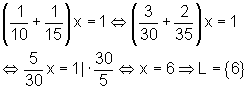
Der Behälter wird in 6 Minuten gefüllt.
5. Ein Schiff wird von 9 Schauerleuten in 5 Tagen gelöscht.
Wie viel Tage würden 15 Schauerleute bei gleicher Arbeitsleistung benötigen?
Ausführliche Lösung mittels Dreisatz:

Das Schiff wird in 3 Tagen gelöscht.
6. Wie alt sind Vater und Sohn, wenn der Vater heute doppelt so alt ist und vor 15 Jahren dreimal so alt war wie sein Sohn?
Ausführliche Lösung:
Der Vater sei heute y Jahre und der Sohn x Jahre alt.
Der Vater ist heute doppelt so alt wie der Sohn: y = 2x
Vor 15 Jahren war der Vater 3 mal so alt wie damals sein Sohn:
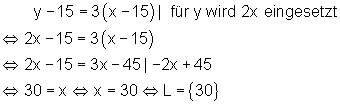
Die Variable x steht für das Alter des Sohnes.
Der Sohn ist 30 Jahre alt, der Vater ist 60 Jahre alt.
7. Drei Freunde haben zusammen 350 € gespart.
A hat doppelt so viel wie B und C nur halb so viel wie B gespart. Wie viel € hat jeder gespart?
Ausführliche Lösung:
Ansatz:
Drei Freunde haben zusammen 350 €:
1. A + B + C = 350 (1)
2. A hat doppelt soviel wie B:
3. A = 2B (2)
4. C hat die Hälfte von B:
5. C = B/2 (3)
Die Gleichung wird so aufgestellt, dass B die Lösungsvariable ist.
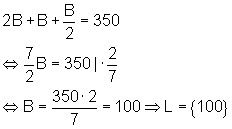
A = 2B = 200 €, B = 100 €, C = B/2 = 50 €.
A hat 200,- €, B hat 100,- €, und C hat 50,- € gespart.
8. Wie groß sind die Seiten eines Rechtecks, dessen Umfang 24 cm beträgt, wenn die eine Seite doppelt so groß ist wie die andere?
Ausführliche Lösung:
Ansatz:
Umfang eines Rechtecks ist:
U =2a + 2b = 24
Eine Seite ist doppelt so groß wie die andere:
a = 2b
Damit lässt sich folgende Gleichung aufstellen:
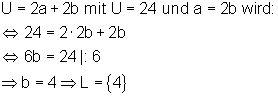
Die Seite b ist 4 cm lang. Wegen a = 2b ist die Seite a 8 cm lang.
Die Rechteckseiten betragen 8 cm und 4 cm.
9. Wird die eine Seite eines Quadrates um 6 cm verkleinert und die andere um 5 cm vergrößert, dann ist der Flächeninhalt des entstandenen Rechtecks um 45 cm2 kleiner als der des Quadrates.
Wie groß ist die Seite des Quadrates?
Ausführliche Lösung:
Ansatz:
Der Flächeninhalt eines Quadrates ist: AQ = a2
Der Flächeninhalt eines Rechtecks ist: AR = ab
Quadratseite a wird um 4 cm verringert und soll im Rechteck a sein: a – 6
Quadratseite a wird um 5 cm verlängert und soll im Rechteck b sein: a + 5
Die Rechteckfläche ist um 45 cm2 kleiner als die Quadratfläche: AR = AQ – 45
Die Lösungsvariable ist a. Damit wird folgende Gleichung aufgestellt:
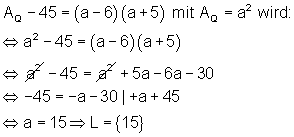
Da die Variable a für die Quadratseite steht, gilt:
Die Quadratseite ist 15 cm lang.
10. Ein Tank hat zwei Zuflussrohre A und B und ein Abflussrohr C.
A füllt den Tank allein in 80 min, B allein in 90 min. Durch C allein kann der Tank in 60 min geleert werden. In welcher Zeit ist der Tank gefüllt, wenn alle drei Rohre zugleich in Tätigkeit sind?
Ausführliche Lösung:
Ansatz:
Das erste Rohr (A) füllt den Tank in einer Minute 1/80.
Das zweite Rohr (B) füllt den Tank in einer Minute 1/90.
Das dritte Rohr (C) entleert den Tank in einer Minute 1/60.
Gesucht ist die Zeit in Minuten, in der der Tank gefüllt wird also die Variable x.
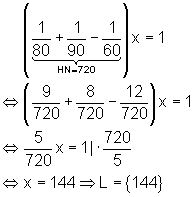
Der Tank ist in 144 Minuten gefüllt.
11. Zwei Autofahrer A und B fahren täglich mit dem Wagen zur Arbeit.
A legt in der Stunde durchschnittlich 54 km, B 72 km zurück. Wann, wie viel Minuten nach Aufbruch von B werden sie sich treffen, wenn A 7 min früher losfährt und beide den gleichen Weg fahren?
Ausführliche Lösung:
Ansatz:
Da nach Minuten gefragt ist, die Geschwindigkeit aber in km/h gegeben ist, wird diese in km/Minute umgerechnet:
Autofahrer A fährt mit der Geschwindigkeit: VA = 54/60 = 0,9 (in km/Minute)
Autofahrer B fährt mit der Geschwindigkeit: VB = 72/60 = 1,2 (in km/Minute)
Gesucht ist die Fahrzeit in Minuten von Fahrer B also tB
Da Fahrer A 7 Minuten vor B startet, ist dieser bis zum Treffpunkt 7 Minuten länger unterwegs also tB +7.
Der Weg zum Treffpunkt ist für beide gleich.

Sie treffen sich nach 21 Minuten.
Die Aufgaben findest du hier.
Hier die dazugehörende Theorie: Lineare Gleichungen zu Sachaufgaben
und hier: Bruchgleichungen lösen.
Hier findest du eine Übersicht über alle Beiträge zum Thema Gleichungen, darin auch Links zu weiteren Aufgaben.

