In diesem Beitrag findet ihr die ausführlichen Lösungen zu den Aufgaben Polynomgleichungen II mit Polynomdivision. In einigen müsst ihr die Gleichung Linearfaktoren zerlegen.
Dabei kann dir sicher eines dieser Videos helfen: Playlist aller Videos zu Polynomgleichungen.
1. a) Berechne die Lösungen folgender Gleichung!
Ausführliche Lösung
Für diese Polynomgleichung soll durch raten eine Lösung gefunden werden. Dazu nimmt man einen Teiler vom Absolutglied (hier einen Teiler von 48). Die Zahl 1 kommt als Lösung nicht in Frage, denn 1 + 4 – 20 -48 = -63 Der Versuch mit x = -2 ergibt -8 +16 +40 – 48 = 0 führt zum Erfolg. Mit der Polynomdivision lässt sich der Grad der Polynomgleichung verringern.
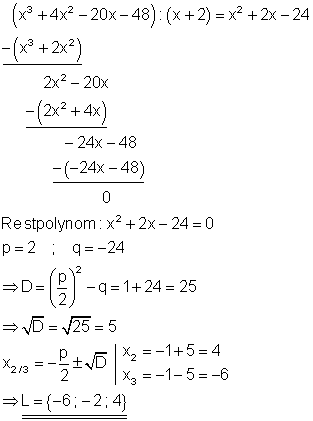
1. b) Berechne die Lösungen folgender Gleichung!
Ausführliche Lösung
Zuerst wird die Polynomgleichung auf die Normalform gebracht. Durch raten erhält man die Lösung x = 2.
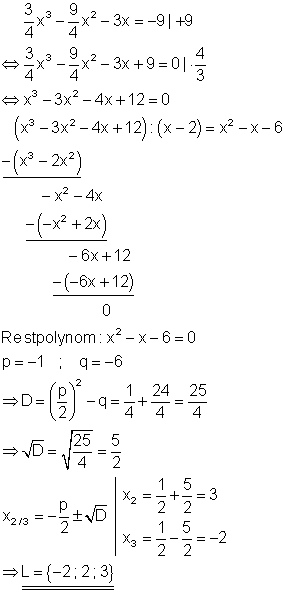
2. a) Berechnen Sie die Lösungen folgender Gleichung!
Ausführliche Lösung
Um eine Lösung durch raten oder probieren zu finden, kann man entweder den Taschenrechner benutzen oder das Horner-Schema verwenden. Hat man eine Lösung für x z. B. mit dem Taschenrechner gefunden, so muss man auf jeden Fall die Polynomdivision durchführen um das Restpolynom zu finden. Hat man hingegen mit dem Horner-Schema einen Lösungswert für x gefunden, so lässt sich aus den Koeffizienten das Restpolynom bilden. Das Horner-Schema liefert also im Schnellverfahren als Abfallprodukt eine Polynomdivision. Nachfolgend soll die erste Lösung mit dem Horner-Schemaa gefunden werden.
Dazu kannst du dir das Video 📽️ Video Horner-Schema: Funktionswerte berechnen ansehen.
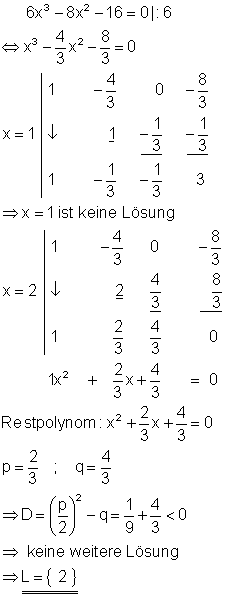
Die erste Zeile im Horner-Schema muss n + 1 Koeffizienten der Polynomgleichung enthalten, wenn der Polynomgrad n ist. Im obigen Beispiel fehlt in der Polynomgleichung der Summand mit dem Exponenten 1 also das x. Im Horner-Schema muss diese Stelle mit 0 aufgefüllt werden. Das Restpolynom hat keine Lösung, da die Diskriminante D < 0 ist.
2. b) Berechne die Lösungen folgender Gleichung!
Ausführliche Lösung
Zuerst wird die Polynomgleichung auf die Normalform gebracht. Durch raten erhält man die Lösung x = -1.
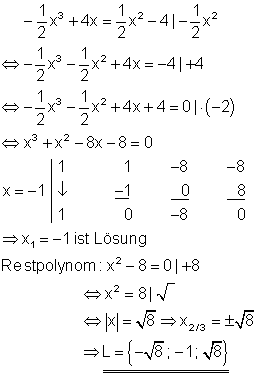
3. a) Berechne die Lösungen folgender Gleichung!
Ausführliche Lösung
Zuerst wird die Polynomgleichung auf die Normalform gebracht. Durch raten erhält man die Lösung x = 2.
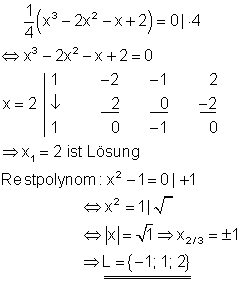
3. b) Berechne die Lösungen folgender Gleichung!
Ausführliche Lösung
Zuerst wird die Polynomgleichung auf die Normalform gebracht. Durch raten erhält man die Lösung x = 1.
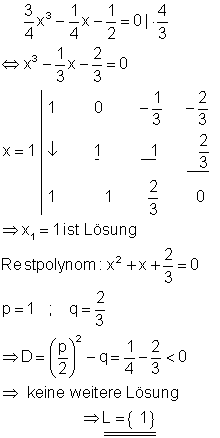
4. a) Berechnen Sie die Lösungen folgender Gleichung!
Ausführliche Lösung
Zuerst wird die Polynomgleichung auf die Normalform gebracht. Durch einsetzen in das Horner-Schema erhält man die Lösung x = 1/2.
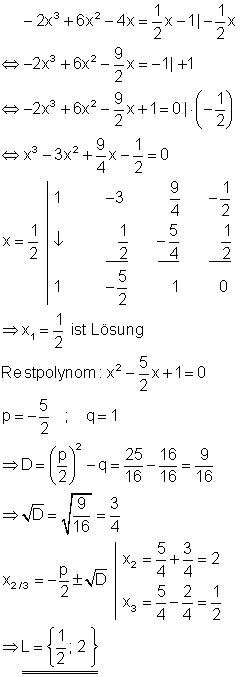
Die Lösung x = 1/2 kommt zweimal vor. In diesem Fall sagt man auch x = 1/2 ist eine zweifache Lösung der Polynomgleichung.
4. b) Berechnen Sie die Lösungen folgender Gleichung!
Ausführliche Lösung
Zuerst wird die Polynomgleichung auf die Normalform gebracht. Durch einsetzen in das Horner-Schema erhält man die Lösung x = 1.
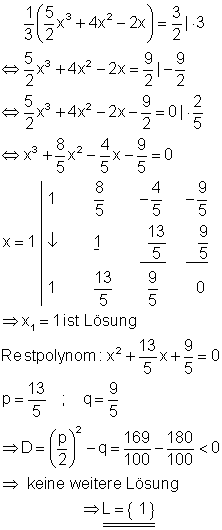
5. a) Berechne die Lösungen folgender Gleichungen für die jeweils eine Lösung bekannt ist.
Führen Sie dazu die Polynomdivision durch!
Ausführliche Lösung
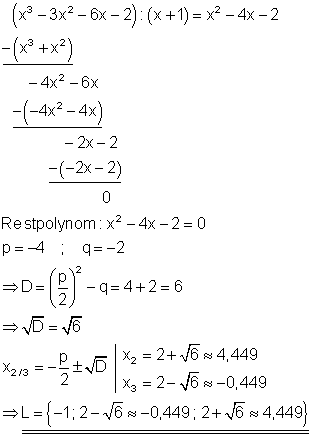
5. b)
Berechne die Lösungen folgender Gleichungen für die jeweils eine Lösung bekannt ist. Führe dazu die Polynomdivision durch!
Ausführliche Lösung
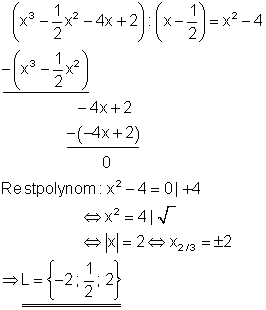
6. a) Führe die Polynomdivision durch!
Ausführliche Lösung
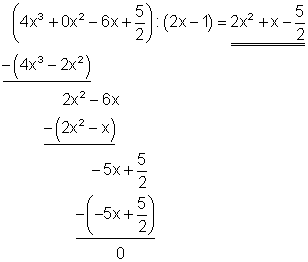
Falls im zu teilenden Polynom ein Summand fehlt, sollte man diesen durch die entsprechende Potenz mit dem Koeffizienten 0 ersetzen (hier 0x2 ). Das vereinfacht die Rechnung.
6. b) Führe die Polynomdivision durch!
Ausführliche Lösung
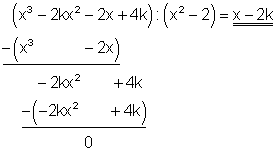
Diese Aufgabe zeigt, wie wichtig es ist die auftretenden Summanden sauber untereinander zu schreiben.
7. Zerlege in Linearfaktoren!
Ausführliche Lösung
Eine Polynomgleichung 3. Grades mit den Lösungen x1 ; x2 und x3 lässt sich auch als Produkt ihrer Linearfaktoren schreiben.
Also: ( x – x1 )( x – x2 )( x – x3 ) = 0. Das gilt in entsprechender Weise für alle Polynomgleichungen beliebigen Grades, falls deren Lösungen bekannt sind. Durch einsetzen in das Horner-Schema erhält man die Lösung x = 1.
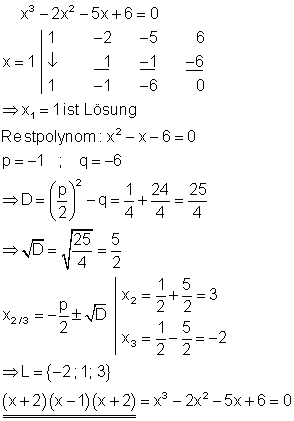
8. Zeige: x = 1 ist doppelte Lösung von x3 -3x + 2!
Ausführliche Lösung
Falls x = 1 doppelte Lösung von x3 -3x + 2 ist, muss gelten:
( x – 1 )( x – 1 )( … ) = ( x – 1 )2 ( … ) = ( x2 – 2x +1 )( … ) = x3 -3x + 2.
Das bedeutet die Polynomdivision (x3 -3x + 2 ):( x2 – 2x +1 ) muss ohne Rest aufgehen. Das Ergebnis liefert sogar eine weitere Lösung.
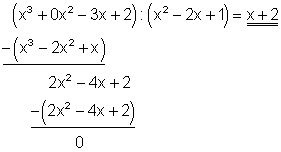
Da die Polynomdivision ohne Rest aufgeht gilt:
Also ( x2 – 2x +1 ) = ( x – 1 )( x – 1 )( x + 2 ) = 0.
Damit wurde gezeigt, das x = 1 eine doppelte Lösung ist.
9. Zeige, dass die Gleichung x3 + kx2 – k2x – k3 =0 nur die Lösungen x1 = k und x2 = -k besitzt!
Ausführliche Lösung
Es ist eine Polynomdivision mit dem Produkt ( x – k )( x + k ) = x2 – k2 durchzuführen.
Das Ergebnis muss entweder ( x – k ) oder ( x + k ) lauten.
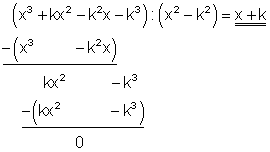
Damit gilt:
x3 + kx2 – k2x – k3 = ( x – k )( x + k )( x + k ) = 0
10. Gegeben ist die Gleichung x3 + (k + 1)x2 – (2k2 – k)x – 2k2 = 0.
Zeige, das x1 = k eine Lösung der Gleichung ist und berechne alle weiteren Lösungen!
Ausführliche Lösung
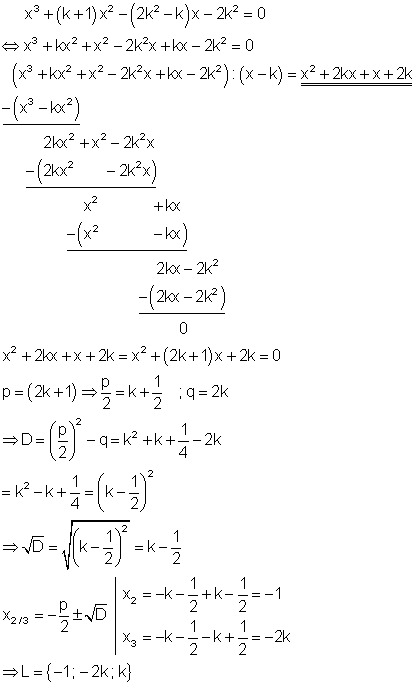
11. Gegeben ist die Gleichung x3 + (k – 1)x2 – (k + 2)x – 2k = 0.
Zeige, das x1 = -1 eine Lösung der Gleichung ist und berechne alle weiteren Lösungen!
Ausführliche Lösung
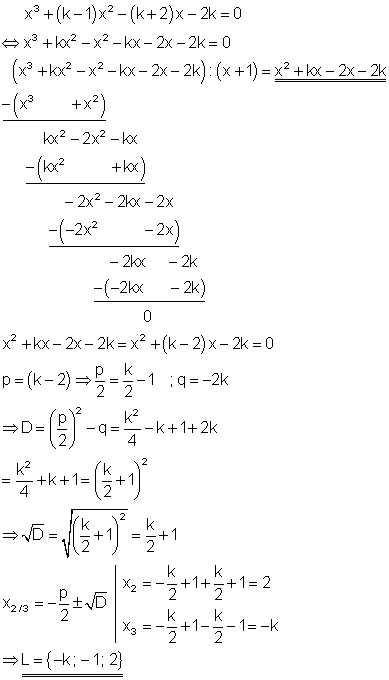
12. Gegeben ist die Gleichung x3 – 4x2 + (k + 4)x – 2k = 0.
Zeige, das x1 = 2 eine Lösung der Gleichung ist. Für welche Werte von k gibt es genau eine weitere doppelte Lösung? Stelle das Ergebnis als Produkt von Linearfaktoren dar!
Ausführliche Lösung
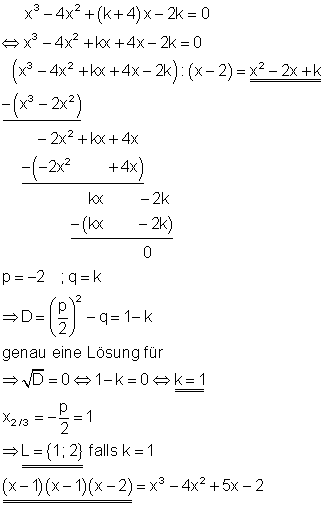
Hier findest dudie Aufgaben.
Und hier die Theorie Polynomgleichungen.
Hier weitere Aufgaben Polynomgleichungen V Text- und Parameteraufgaben.
Hier findest du eine Übersicht über alle Beiträge zum Thema Gleichungen, dort auch Links zu weiteren Aufgaben.

