Bis jetzt haben wir Funktionen kennengelernt, bei denen die Variable x in der 2. Potenz steht. Deshalb nennt man solche Funktionen quadratische Funktion oder auch ganzrationale Funktionen 2. Grades. Die Variable x kann allerdings in jeder Potenz auftreten. Diese Funktionen nennen wir deshalb Potenzfunktionen. Zuerst erkläre ich die Definition der Potenzfunktion. Danach stelle ich Beispiele zu Potenzfunktionen 1. bis 4. Grades mit den dazugehörenden Graphen vor. Anschließend können Sie Ihr Wissen mit Testfragen zu den Eigenschaften von Potenzfunktionen prüfen. Schließlich erkläre ich, wann eine Potenzfunktion symmetrisch ist. Hierzu stelle ich Trainingsaufgaben. Zuletzt stelle ich einen interaktiven Rechner für ganzrationale Funktionen bis 9. Grades zur Verfügung.
Dazu könnt ihr euch dieses 📽️ Video Potenzfunktionen Symmetrie, Verlauf, Wertebereich ansehen.
Definition Potenzfunktion:
Eine Funktion mit der Funktionsgleichng f(x) = a_n x^n ; n ∈ ℕ ; a_n ∈ ℝ heißt Potenzfunktion. Mit anderen Worten: x kommt nur einmal in einer Potenz vor. Dabei bestimmt der Exponent n den Grad der Potenzfunktion. Und der Faktor a_n die Form des Graphen, deshalb nennt man ihn Formfaktor.
Hier Beispiele zu Potenzfunktionen 1. bis 4. Grades mit den dazugehörenden Graphen:
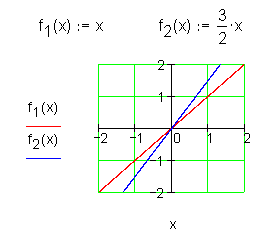
Gerade: Potenzfunktion 1. Grades
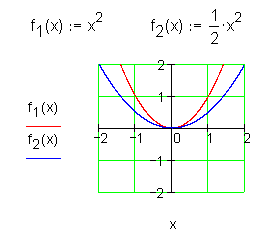
Parabel: Potenzfunktion 2. Grades
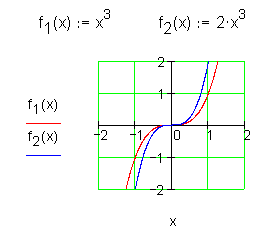
Potenzfunktion 3. Grades
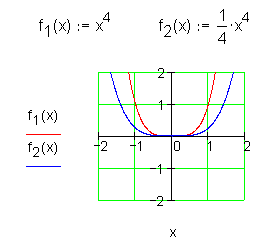
Potenzfunktion 4. Grades
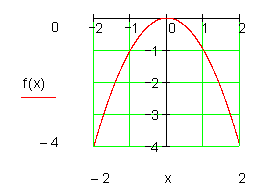
Wie lautet die Funktionsgleichung?
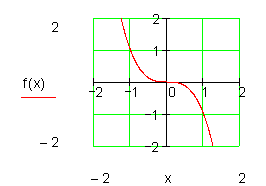
Wie lautet die Funktionsgleichung?
Testfragen zu Potenzfunktionen:
a) Welche gemeinsamen Punkte haben die Graphen?
b) Welchen Einfluss hat der Grad n und das Vorzeichen von an auf den Verlauf des Graphen?
c) Welchen Einfluss hat der Grad n der Potenzfunktion auf die Symmetrie des Graphen?
d) Welche Wertemengen in Abhängigkeit von n und dem Vorzeichen von an haben Potenzfunktionen?
e) Welchen Einfluss hat der Betrag von an auf den Verlauf der Graphen?
Die Antworten findest du am Ende der Seite.
Symmetrie bei Potenzfunktionen
Wie lässt sich die Symmetrie beurteilen, wenn man nur die Funktionsgleichung einer Potenzfunktion kennt?
Dazu zeichnen wir die Graphen folgender Funktionen:

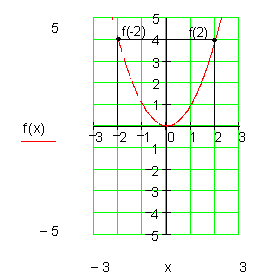
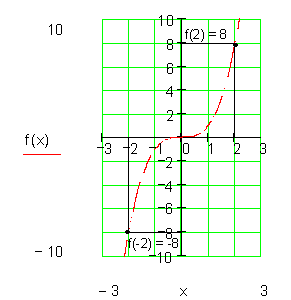
Die Vermutung liegt nahe, dass folgendes gilt:
Für gerade Exponenten von x sind die Funktionswerte gleich.
Das nennt man Achsensymmetrie, also f(-x) = f(x)
Für ungerade Exponenten von x haben die Funktionswerte den gleichen Betrag aber entgegengesetztes Vorzeichen.
Das nennt man Punktsymmetrie, also f(-x) = – f(x)
Dieser Zusammenhang gilt für alle Potenzfunktionen (hier ohne Beweis).
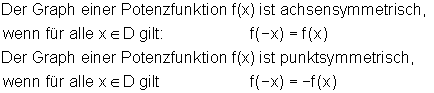
Zusammenfassung:
Tabelle mit Beispielen:
| n gerade | n ungerade | |
| an>0 | Verlauf von II nach I
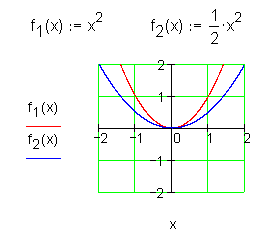
| Verlauf von III nach I
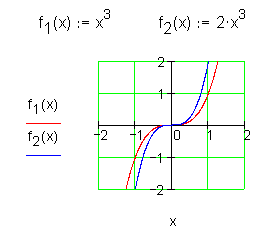
|
| an<0 | Verlauf von III nach IV
f(x) = -x^2 
| Verlauf von II nach IV |

Für an > 0 gilt:
Alle Potenzfunktionen mit geraden Exponenten sind achsensymmetrisch. Sie verlaufen vom II. in den I. Quadranten.
Alle Potenzfunktionen mit ungeraden Exponenten sind punktsymmetrisch. Sie verlaufen vom III. in den I. Quadranten.
Für an < 0 gilt:
Alle Potenzfunktionen mit geraden Exponenten sind achsensymmetrisch. Sie verlaufen vom III. in den IV. Quadranten.
Alle Potenzfunktionen mit ungeraden Exponenten sind punktsymmetrisch. Sie verlaufen vom II. in den IV. Quadranten.
Dazu könnt ihr euch dieses 📽️ Video Potenzfunktionen Symmetrie, Verlauf, Wertebereich ansehen.
Antworten zu den Fragen:
zu a) Alle Graphen verlaufen durch die Punkte ( 0 | 0 )
zu b) n gerade und an > 0: Der Graph verläuft vom II. zum I. Quadranten.
n gerade und an < 0: Der Graph verläuft vom III. zum IV. Quadranten.
n ungerade und an > 0: Der Graph verläuft vom III. zum I. Quadranten.
n ungerade und an < 0: Der Graph verläuft vom II. zum IV. Quadranten.
zu c) n gerade: Der Graph ist symmetrisch zur y- Achse (Achsensymmetrie)
n ungerade: Der Graph ist symmetrisch zum Koordinatenursprung (Punktsymmetrie)
zu d) n gerade und an > 0: f(x) ≥ 0 Es gibt nur positive Funktionswerte einschließlich der Null.
n gerade und an < 0: f (x) ≤ 0 Es gibt nur negative Funktionswerte einschließlich der Null.
n ungerade und an > 0: Wertemenge W = IR
n ungerade und an < 0: Wertemenge W = IR
zu e) Der Faktor an bestimmt die jeweilige Form des Graphen (gestreckt oder gestaucht), deshalb wird er auch Formfaktor genannt. Eine Vorzeichenänderung bewirkt die Spiegelung an der x-Achse.
Rechner für ganzrationale Funktionen bis 9. Grades
Interaktiv: Gib die Koeffizienten der Funktionsgleichung ein, danach zeichnet das Javascript den Graph der Funktion.
Aufgaben:
Eigenschaften von Potenzfunktionen.
Bestimme den Grad folgender Potenzfunktionen, mach eine Aussage über das Symmetrieverhalten, den Verlauf des Graphen und die Wertemenge. Zeichne die Graphen jeweils in ein Koordinatensystem.
1.![]()
2.![]()
3.![]()
4.![]()
5.![]()
6.![]()
7.![]()
8.![]()
9.![]()
10.![]()
Dazu findest du hier die Lösungen.
Weitere Aufgaben hierzu: Aufgaben Ganzrationale Funktionen I Eigenschaften von Potenzfunktionen.
Hier findest du eine Übersicht über alle Beiträge zum Thema weitere ganzrationale Funktionen, darin auch Links zu weiteren Aufgaben.
