Hier findest du die Lösungen der Aufgaben zur Vorbereitung einer Klassenarbeit zum Thema quadratische Funktionen Teil II mit komplettem Lösungsweg.
Dabei können diese Videos dir helfen Playlist: Alle Videos zu quadratischen Funktionen.
1. Berechne die Lösungen folgender quadratischen Gleichungen!
Ausführliche Lösungen
a)
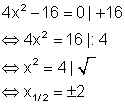
b)
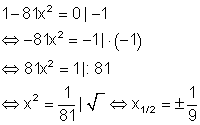
c)
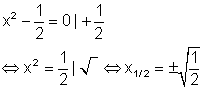
d)
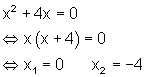
e)
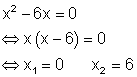
f)
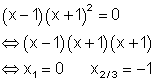
2. Forme die Gleichung um und berechne x!
Ausführliche Lösung
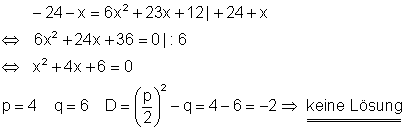
Der Wert der Diskriminante lässt eine Aussage über die Anzahl und Art der Lösungen einer quadratischen Gleichung zu:
Wenn D > 0 Die quadratische Gleichung hat zwei Lösungen.
D = 0 Die quadratische Gleichung hat eine Lösung.
D < 0 Die quadratische Gleichung hat keine Lösung.
3. Löse folgende quadratische Gleichungen!
Ausführliche Lösungen
a)
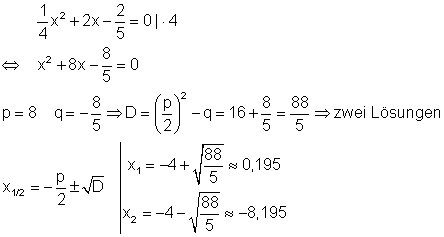
b)
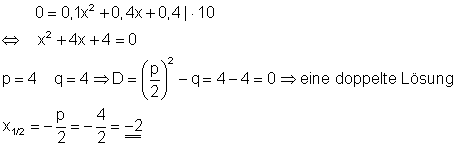
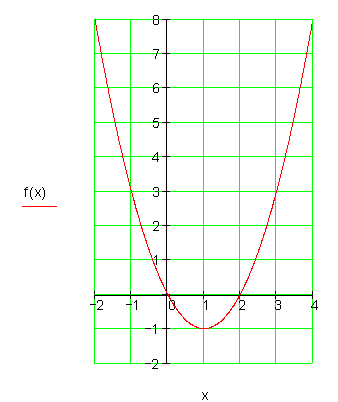
4. Berechne den Scheitelpunkt
und die Achsenschnittpunkte und zeichne die Parabel in ein geeignetes Koordinatensystem!
Ausführliche Lösungen
a)
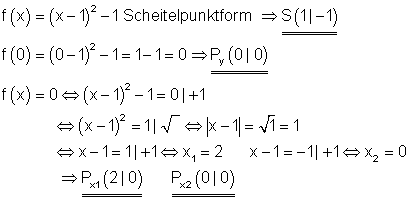
b)
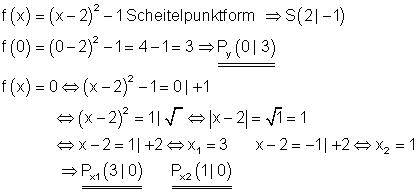
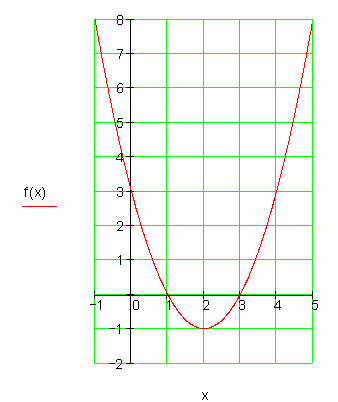
5. Berechne
von folgenden quadratischen Funktionen die Achsenschnittpunkte, den Scheitelpunkt und die Scheitelpunktform der Funktionsgleichung! Wie ist die Parabel aus der Normalparabel entstanden? Zeichne den Graphen in ein Koordinatensystem.
Ausführliche Lösungen
a)
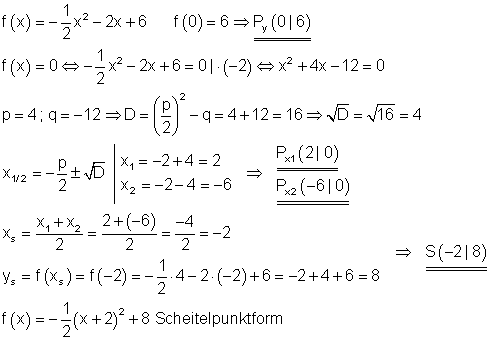
Normalparabel, um den Faktor 1/2 gestaucht und nach unten geöffnet. Verschiebung um 2 EH nach links. Verschiebung um 8 EH nach oben.
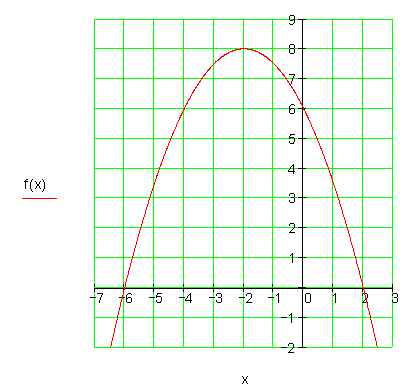
b)
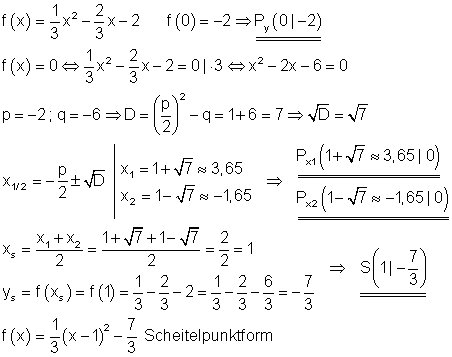
Normalparabel, um den Faktor 1/3 gestaucht und nach oben geöffnet. Verschiebung um 1 EH nach rechts. Verschiebung um 7/3 EH nach unten.
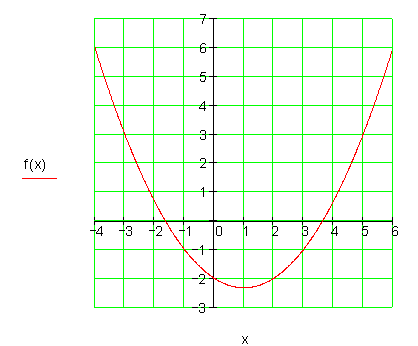
6. Der Kraftstoffverbrauch
eines PKW hängt bekanntlich von der Geschwindigkeit ab. Durch Messungen wurde der funktionale Zusammenhang ermittelt.
Ausführliche Lösungen
a)
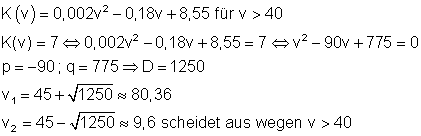
Bei einer Geschwindigkeit von 80,36 km/h ist der Verbrauch 7 Liter/100 km.
b)
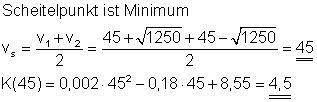
Bei einer Geschwindigkeit von 45 km/h ist der Verbrauch mit 4,5 Liter/ 100 km am geringsten.
7. Beschreibe
schrittweise, wie f(x) aus der Normalparabel entsteht und wie sie geöffnet ist. Welche Koordinaten hat der Scheitelpunkt?
Ausführliche Lösungen
a) Normalparabel verschoben um 2 EH nach links, um 9 EH nach unten, nach oben geöffnet. Der Scheitelpunkt hat die Koordinaten:
![]()
b) Normalparabel verschoben um 4 EH nach rechts, um 3 EH nach unten, nach oben geöffnet, um den Faktor 1/2 gestaucht. Der Scheitelpunkt hat die Koordinaten:
![]()
c) Normalparabel verschoben um 3/2 EH nach rechts, um 5/4 EH nach oben, nach unten geöffnet, um den Faktor 7/3 gestreckt. Der Scheitelpunkt hat die Koordinaten:
![]()
d) Normalparabel verschoben um 3/4 EH nach links, um 1/3 EH nach unten, nach unten geöffnet, um den Faktor 4 gestreckt. Der Scheitelpunkt hat die Koordinaten.
![]()
8. Bestimme
den größten bzw. kleinsten Wert der Funktion f(x).
Ausführliche Lösungen
a)

b)

9. Welches Rechteck
mit dem Umfang U = 18 cm hat den größten Flächeninhalt?
Ausführliche Lösung
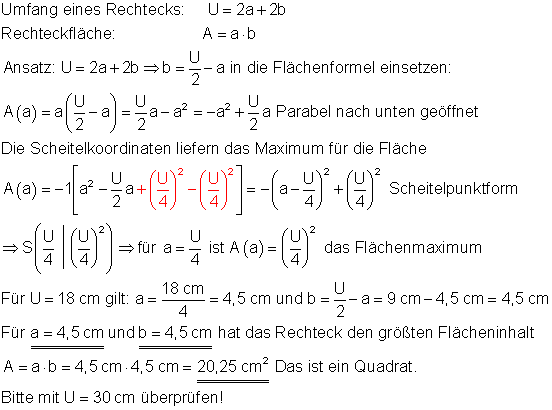
Hier findest du die Aufgaben
hier die dazugehörige Theorie: Zusammenfassung Quadratische Funktionen
und hier eine Übersicht über weitere Beiträge zu quadratische Funktionen.

