Hier findest du die Lösungen zu den Aufgaben mit ganzrationalen Funktionen I, darum geht es um die Eigenschaften von Potenzfunktionen.
1.
Betrachte die Graphen nebenstehender Potenzfunktionen im 1. Quadranten!
Für x-Werte zwischen 0 und 1 liegt der Graph einer Potenzfunktion höheren Grades unterhalb des Graphen einer Potenzfunktion niederen Grades.
Für x > 1 ist das genau umgekehrt.
Begründe dieses Verhalten!
Ergebnis:
Multipliziert man eine Zahl, die kleiner als 1 ist, mit sich selbst, wird das Ergebnis immer kleiner.
Multipliziert man eine Zahl, die größer als 1 ist, mit sich selbst, wird das Ergebnis immer größer.
2.
Der Graph der Potenzfunktion 3. Grades soll um 2 Einheiten nach links und anschließend um 3 Einheiten nach oben verschoben werden.
Gib die Funktionsgleichung für den verschobenen Graphen an!
Ausführliche Lösung
3.
Der Graph der Potenzfunktion vierten Grades soll um 3 Einheiten nach rechts verschoben und anschließend um den Faktor 2 gestreckt werden.
a) Gib die Funktionsgleichung für den verschobenen Graphen an!
b) Weise nach, dass der Graph weder achsen- noch punktsymmetrisch ist!
Ausführliche Lösung
a)
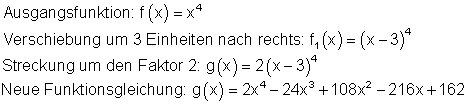
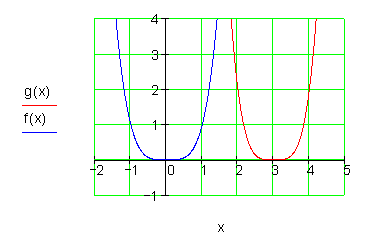
b)

4.
Bei welcher Potenzfunktion f(x) = xn gehört der Punkt P zum Graphen?
Gib die Gleichung dieser Potenzfunktion an!
a) P(-3 | -27)
b) P(-2 | 16)
c) P(0,5 | 0,25)
d)
![]()
e) P(0,1 | 0,0001)
f) P(-1| 1)
g) P(-2 | 8)
h)
![]()
Ergebnisse:
a)
![]()
b)
![]()
c)
![]()
d)
![]()
e)
![]()
f)
![]()
g)

h)
![]()
5.
Bestimme die Symmetrie und den Verlauf der Graphen folgender Potenzfunktionen und gib jeweils die Wertemenge und den Grad an!
Ergebnisse
a)
![]()
b)
![]()
c)
![]()
d)
![]()
e)
![]()
f)
![]()
6.
Stelle folgende Funktionsgleichungen durch Polynome dar!
Gib jeweils den Grad an!
Ergebnisse:
a)
![]()
b)
![]()
c)
![]()
d)
![]()
e)
![]()
f)
![]()
7.
Begründe: Der Graph einer ganzrationalen Funktion mit ungeradem Grad schneidet die x-Achse mindestens einmal!
Gilt das auch wenn der Grad gerade ist?
Ausführliche Lösung:
Der Graph einer ganzrationalen Funktion mit ungeradem Grad verläuft entweder von III nach I oder von II nach IV. Dabei wird in jedem Fall die x- Achse mindestens einmal geschnitten (mind. eine Nullstelle).
Der Graph einer ganzrationalen Funktion mit geradem Grad verläuft entweder von II nach I oder von III nach IV. Dabei wird die x- Achse nicht notwendigerweise geschnitten (keine Nullstelle).
Hier findest du die Aufgaben hierzu.
Und hier weitere Aufgaben: Aufgaben Ganzrationale Funktionen II
Potenzfunktionen und deren Eigenschaften.
Hier findest du eine Übersicht über alle Beiträge zum Thema weitere ganzrationale Funktionen, darin auch Links zu weiteren Aufgaben.