Hier findest du die Lösungen der Aufgaben zu linearen Funktionen, z. B. den günstigsten Stromanbieter finden.
1. Der Schnellimbiss „MC- Pommes“
benötigt für die Fritteusen täglich 19 kg frisches Fett.Momentan sind noch 250 kg im Lager vorhanden.
a) Stelle die Funktionsgleichung auf und zeichne den Graphen in ein geeignetes Koordinatensystem!
b)mBei einem Lagerbestand von 95 kg soll der Filialleiter nachbestellen. Nach wie viel Tagen muss die Bestellung erfolgen?
c) Wie lange reicht das Fett, wenn nicht nachbestellt wird?
Ausführliche Lösungen
a)
Die unabhängige Variable x steht für die Zeit in Tagen.
Die abhängige Variable f(x) steht für die verbleibende Menge Fett in kg.
Der Anfangswert beträgt 250 kg.
Die Änderungsrate ist negativ und beträgt 19 kg/Tag.
Da ein linearer Zusammenhang besteht gilt:
f(x) = a1x + a0 mit a1 = -19 und a0 = 250 wird
f(x) = -19x + 250.
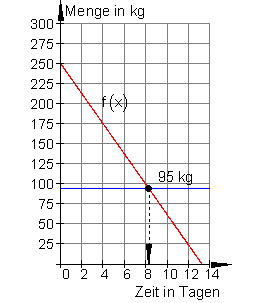
b)
Da bei 95 kg nachbestellt werden soll, gilt der Ansatz:
f(x) = 95 \Leftrightarrow -19x + 250 = 95 | \cdot (-1) \\
\Leftrightarrow 19x - 250 = -95 | +250 \\
\Leftrightarrow 19x = 155 | : 19 \\
\Leftrightarrow x = \frac{155}{19} \approx 8,156
Die Bestellung muss in etwa 8 Tagen erfolgen.
c)
Zu bestimmen ist der Schnittpunkt des Graphen mit der y-Achse:
f(x) = 0 \Leftrightarrow -19x + 250 = 0 | \cdot (-1) \\
\Leftrightarrow 19x - 250 = 0 | +250 \\
\Leftrightarrow 19x = 250 | : 19 \\ \Leftrightarrow x = \frac{250}{19} \approx 13,158
Das Fett reicht noch etwa 13 Tage.
2. Ponyhof
Die Pferdeställe auf dem Ponyhof „Robinson“ müssen in bestimmten Zeitabständen ausgemistet und mit frischem Stroh versorgt werden.
Dabei fallen täglich 2,5 m3 Mist an. Der Misthaufen hat momentan ein Volumen von 11 m3. Maximal können 50 m3 Mist gelagert werden.
a) Stelle eine Funktionsgleichung auf, die diesen Sachverhalt beschreibt und zeichne den dazugehörigen Graphen in ein geeignetes Koordinatensystem!
b) Nach welcher Zeit muss der Mist abgefahren werden?
c) Vor wie vielen Tagen wurde das letzte Mal Mist abgefahren?
Ausführliche Lösungen
a)
Die unabhängige Variable x steht für die Zeit in Tagen.
Die abhängige Variable f(x) steht für die Menge Mist in m3.
Der Anfangswert beträgt 11 m3.
Die Änderungsrate ist positiv und beträgt 2,5 m3/Tag.
Da ein linearer Zusammenhang besteht gilt:
f(x) = a1x + a0 mit a1 = 2,5 und a0 = 11 wird
f(x) = 2,5x + 11.
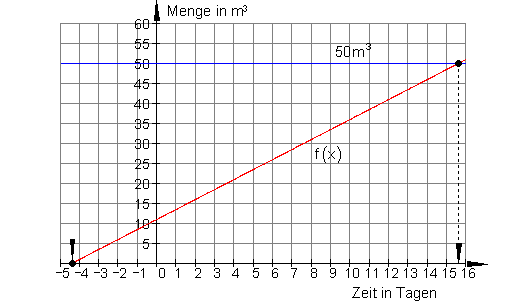
b)
Zu bestimmen ist die Zeit, nach der das Mistaufkommen auf 50 m3 angewachsen ist.
f(x) = 50 \Leftrightarrow 2,5x + 11 = 50 | -11 \\
\Leftrightarrow 2,5x = 39 | : 2,5 \\
\Leftrightarrow x = \frac{78}{5} = \underline{\underline{15,6}}
Nach etwa 15 Tagen muss der Mist abgefahren werden.
c)
Der x- Wert des Schnittpunktes des Graphen mit der x- Achse im negativen Bereich gibt an wann der Mist zuletzt abgefahren wurde.
f(x) = 0 \Leftrightarrow 2,5x + 11 = 0 | -11 \\
\Leftrightarrow 2,5x = -11 | : 2,5 \\
\Leftrightarrow x = -\frac{22}{5} = \underline{\underline{-4,4}}
Vor etwas mehr als 4 Tagen wurde das letzte Mal der Mist abgefahren.
3. Telefonanbieters
Wie man eine ähnliche Aufgabe löst kannst du dir in dem 📽️Video Lineare Funktion günstigster Strom Textaufgabe ansehen.
Armin sieht sich die Tarife des Telefonanbieters „Billigsurf“ an.
1.Tarif A: Grundgebühr 5 € / Monat die ersten 10 Stunden frei, dann 0,5 Ct. / min.
2. Tarif B: Grundgebühr 10 € / Monat die ersten 20 Stunden frei, dann 0,4 Ct. / min.
3. Tarif C: Flatrate 25 € / Monat.
Durchschnittlich surft Armin zweieinhalb Stunden täglich.
a) Stelle für jeden Tarif die Funktionsgleichung auf!
b) Zeichne die Funktionsgraphen in ein geeignetes Koordinatensystem!
c) Erkläre, was alles aus den Graphen ablesbar ist (Interpretation)!
d) Berechne den günstigsten Tarif für Armin!
e) In welchem Punkt herrscht Kostengleichheit für Tarif A und B?
f) Ab welcher Surfzeit sollte Armin die Flatrate wählen?
Ausführliche Lösungen
a)
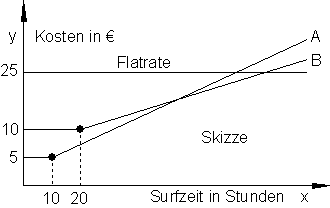
x-Achse Zeit in Stunden y-Achse Kosten in
Tarif A:
0,5 \frac{Cent}{min} \quad sind \quad 60 min \cdot 0,5 \frac{Cent}{min} = \\
30 \frac{Ct}{h} = 0,3 \frac{€}{h} \quad (Steigung) \\
\Rightarrow K_A(x) = 0,3x + a_0
10 Freistunden bedeuten, in den ersten 10 Stunden fallen nur die Grundgebühren von 5 € an.
\Rightarrow P(10 | 5)
Durch diesen Punkt verläuft der Graph von K_A(x). \\
P(10 | 5) \Rightarrow K_A(10) = 5 \\
\Leftrightarrow 0,3 \cdot 10 + a_0 = 5 | -3 \\
\Leftrightarrow a_0 = 2
Funktionsgleichung für Tarif A: \color{red}{ K_A(x) = 0,3x + 2}
Tarif B:
0,4 \frac{Cent}{min} \quad sind \quad 60 min \cdot 0,4 \frac{Cent}{min} = \\
24 \frac{Ct}{h} = 0,24 \frac{€}{h} \quad (Steigung) \\
\Rightarrow K_B(x) = 0,24x + a_0
20 Freistunden bedeuten, in den ersten 20 Stunden fallen nur die Grundgebühren von 10 € an.
\Rightarrow P(20 | 10)
Durch diesen Punkt verläuft der Graph von K_B(x). \\
P(20 | 10) \Rightarrow K_B(20) = 10 \\
\Leftrightarrow 0,24 \cdot 20 + a_0 = 10 | -4,8 \\
\Leftrightarrow a_0 = 5,2
Funktionsgleichung für Tarif B: \color{blue}{ K_B(x) = 0,24x + 5,2}.
Tarif C: Flatrate 25 € ist unabhängig von der Surfzeit.
Funktionsgleichung für Tarif C: F(x) = 25 (Parallele zur x-Achse).
b)
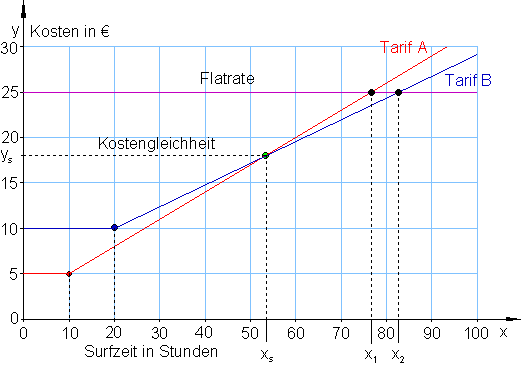
c)
Bei etwa 53 Stunden schneiden sich beide Geraden, in dem Punkt herrscht Kostengleichheit. Bis etwa 53 Stunden ist Tarif A der günstigste. Zwischen etwa 53 und 82 Stunden ist Tarif B der günstigste. Ab etwa 82 Stunden lohnt sich die Flatrate.
d)
Armin surft etwa 75 Stunden im Monat. Für ihn wäre bei dieser Surfdauer Tarif B der günstigste. Eine Rechnung soll das belegen:
Monatliche Surfdauer 2,5 h · 30 = 74 Stunden.
Kosten bei Tarif A: KA(75) = 0,3 · 75 + 2 = 24,50.
Kosten bei Tarif B: KB(75) = 0,24 ·75 + 5,2 = 23,20.
Kosten bei Tarif C: F(75) = 25.
e)
Kostengleichheit für Tarif A und B ist im Schnittpunkt beider Geraden zu finden.
K_A(x) = K_B \\
\Leftrightarrow 0,3x + 2 = 0,24x + 5,2 | -0,24x \\
\Leftrightarrow 0,06x + 2 = 5,2 | - 2 \\
\Leftrightarrow 0,06x = 3,27 | : 0,06 \\
\Leftrightarrow x = x_s = \frac{320}{100} : \frac{6}{100} = \frac{320 \cdot 100}{100 \cdot 6} = \frac{320}{6} = \\
\frac{160}{3} = 53 \frac{1}{3} (53 Stunden und 20 Minuten).
K_A(\frac{160}{3}) = \frac{3}{10} \cdot \frac{160}{3} +2 = 16 + 2 = 18 .
Kostengleichheit herrscht bei einer Surfzeit von 53 h und 20 min. Die für diese Zeit anfallenden Kosten betragen für beide Tarife 18 €.
f)
Aus den Graphen ist abzulesen, dass der Schnittpunkt von KB (x) mit F (x) den Punkt markiert, ab dem für längere Surfzeiten die Flatrate günstiger ist als Tarif B.
K_B(x) = F(x) \\ \Leftrightarrow 0,24x + 5,2 = 25 | - 5,2 \\ \Leftrightarrow 0,24x = 19,8 | : 0,24 \\ \Leftrightarrow x = x_2 = 82,5 .
Ab einer Surfdauer von 82,5 Stunden monatlich, sollte man auf die Flatrate umstellen.
4. Handyvertrag
Holger und Ali haben die Vertragskonditionen für ihre Handys nie gelesen.
Beide behaupten, sie hätten jeweils den günstigsten Vertrag und stützen sich dabei auf folgende Daten:
Holger zahlt 10,10 €, wenn er im Monat 30 Minuten telefoniert und 13,70 € bei 60 Minuten.
Ali zahlt 10,80 €, wenn er im Monat 40 Minuten telefoniert und 15,20 € bei 80 Minuten.
a) Stelle für beide Verträge die Funktionsgleichungen auf!
b) Zeichne beide Graphen in ein geeignetes Koordinatensystem!
c) Wer von beiden hat den günstigsten Vertrag? Begründe dein Ergebnis!
Ausführliche Lösungen
a)
Holger: 30 min 10,10 €
60 min 13,70 €
K_1(x) = a_1x + a_0 \\
P_1(30 | 10,1) \quad P_2(60 | 13,7) \\
a_1 = \frac{y_2 - y_1}{x_2 - x_1} = \frac{13,7 - 10,1}{60 - 30} = \frac{3,6}{30} = 0,12 \\
K_1(x) = 0,12x + a_0 \quad mit \quad P_1(30 | 10,1) \\
K_1(30) = 10,1 \\
\Leftrightarrow 0,12 \cdot 30 + a_0 = 10,1 \\
\Leftrightarrow 3,6 + a_0 = 10,1 | - 3,6 \\ \Leftrightarrow a_0 = 6,5 \\
\underline{\underline{K_1(x) = 0,12x + 6,5}} .
Ali: 40 min 10,80 €
80 min 15,20 €
K_2(x) = a_1x + a_0 \\
P_1(40 | 10,8) \quad P_2(80 | 15,2) \\
a_1 = \frac{y_2 - y_1}{x_2 - x_1} = \frac{15,2 - 10,8}{80 - 40} = \frac{4,4}{40} = 0,11 \\
K_2(x) = 0,11x + a_0 \quad mit \quad P_1(40 | 10,8) \\
K_2(40) = 10,8 \\
\Leftrightarrow 0,11 \cdot 40 + a_0 = 10,8 \\
\Leftrightarrow 4,4 + a_0 = 10,8 | - 4,4 \\ \Leftrightarrow a_0 = 6,4 \\
\underline{\underline{K_2(x) = 0,11x + 6,4}} .
b)
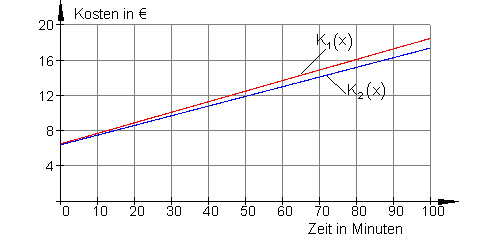
c)
Ali hat den günstigsten Vertrag, denn seine Kostenkurve K2(x) liegt immer unterhalb der von Holger.
Die beiden Geraden schneiden sich auch nicht im positiven x- Bereich, da die Steigung von K2(x) geringer ist als die von K1(x), wird mit zunehmender Gesprächsdauer der Kostenunterschied immer größer.
Der Schnittpunkt der Geraden liegt im negativen x- Bereich und hat in Bezug auf die Aufgabenstellung keine Bedeutung.
5. Energieversorger
Ein Tarifmodell eines Energieversorgers setzt sich aus einer monatlichen Grundgebühr G und den Verbrauchskosten p pro kWh zusammen.
Dabei entsteht ein linearer Zusammenhang: K(x) = p · x + G.
Folgende Tarife stehen zur Verfügung:
| Tarife | monatliche Grundgebühr in € | Preis pro kWh in € |
|---|---|---|
| Tarif I | 11,80 | 0,157 |
| Tarif II | 9,00 | 0,172 |
| Tarif III | 18,50 | 0,125 |
a) Stelle für jeden Tarif die Funktionsgleichung auf und zeichnen Sie die dazugehörigen Graphen in ein Koordinatensystem.
b) Finde für den monatlichen Verbrauch von 800 kWh einer Durchschnittsfamilie den günstigsten Stromanbieter.
c) Welche Bedeutung haben die Schnittpunkte der Geraden im Koordinatensystem?
Ausführliche Lösungen
a)
Die Funktionsgleichungen:
Tarif I: K_1(x) = 0,157x + 11,80 \\
Tarif II: K_2(x) = 0,172x + 9,00 \\
Tarif II: K_3(x) = 0,135x + 14,40 \\
Tarif III: K_4(x) = 0,125x + 18,50
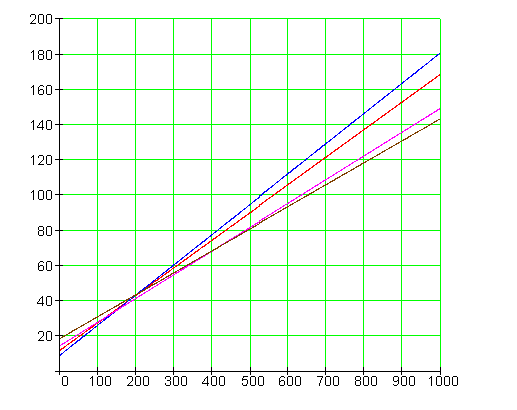
b)
Tarif I: K_1(800) = 0,157 \cdot 800 + 11,80 = \underline{\underline{137,40}}
Tarif II: K_2(800) = 0,172 \cdot 800 + 9,00 = \underline{\underline{146,60}}
Tarif II: K_3(800) = 0,135 \cdot 800 + 14,40 = \underline{\underline{122,40}}
Tarif II: K_4(800) = 0,125 \cdot 800 + 18,50 = \underline{\underline{118,50}}
Bei einem monatlichen Verbrauch von 800 kWh ist Tarif IV der günstigste.
c)
Immer da wo sich zwei Graphen schneiden entstehen für einen bestimmten Verbrauch die gleichen Kosten.
6.Gegeben ist die lineare Funktion f(x) = 0,4x – 2 . Der Funktionsgraph wird um 4 Einheiten in Richtung der positiven x- Achse verschoben. Bestimmen Sie den Funktionsterm g(x) der verschobenen Geraden. Wie lässt sich g(x) noch aus f(x) erzeugen?
Ausführliche Lösung:
f(x) = 0,4x - 2 Verschiebung um 4 Einheiten nach rechts bedeutet:
g(x) = \underline{\underline{0,4(x - 4) - 2 = 0,4x - 3,6}}
Das gleiche Ergebnis erhält man durch eine Verschiebung um 1,6 Einheiten nach unten.
Hier findest du die Aufgaben.
Hier weitere Aufgaben Lineare Funktionen Aufgaben XVII Textaufgaben.
Theorie hierzu: Einführung lineare Funktionen.
Und Textaufgaben zu linearen Funktionen.
Hier eine Übersicht über alle Beiträge zur Linearen Funktionen, dort auch Links zu weiteren Aufgaben.

