In diesem Beitrag zeige ich zuerst anhand eines Beispiels, was die Streuung um den Mittelwert bedeutet. Im letzten Beitrag Mittelwert, Median und Modalwert hatten wir uns mit der Mitte einer Datenreihe beschäftigt. Wenn der Mittelwert zweier Gruppen gleich groß ist, können die Einzelwerte sehr unterschiedlich verteilt sein. Mit anderen Worten: dies ist eine Streuung. Dies misst man mit Spannweite, Varianz und Standardabweichung, Quartile, Quartilsabstand und Boxplot.
- Streuung um den Mittelwert
- Spannweite
- Quartile und Quartilsabstand
- Vergleich zwischen Quartilsabstand und Spannweite
- Definition Boxplot
- Varianz: Definition und Berechnung
- Standardabweichung: Definition und Berechnung
- Zuletzt verlinke ich zu Aufgaben und weiteren Beiträgen
Streuung um den Mittelwert
Beispiel:
Im Folgenden ist die Notenverteilung zweier Schülergruppen dargestellt, deren Mittelwert gleich sind.
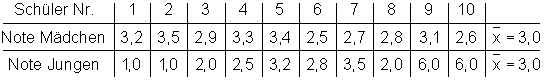
Säulendiagramm Notenverteilung Mädchen
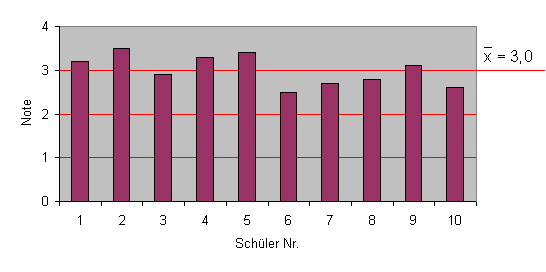
Säulendiagramm Notenverteilung Jungen
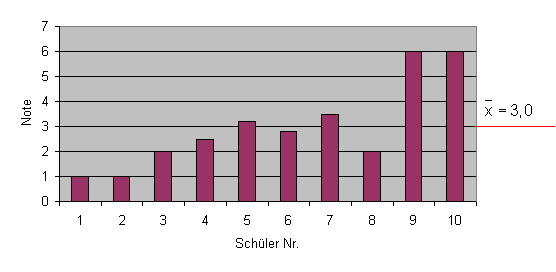
Aber wir sehen sofort, dass bei den Mädchen die Noten alle sehr nahe am Mittelwert liegen. Mit anderen Worten: Sie streuen wenig um den Mittelwert.
Bei den Jungen dagegen sind die Abweichungen vom Mittelwert sehr groß. Das heißt, sie streuen stark um den Mittelwert.
Die Statistik bietet deshalb ein Maß, um die Streuung zu messen.
Die Spannweite
Wenn man den Unterschied zwischen dem größten und kleinsten Beobachtungswert berechnet, erhält man die Spannweite.
Mit ihr misst man die Breite des Streubereichs einer Häufigkeitsverteilung.
Definition Spannweite:
Spannweite = größter Beobachtungswert – kleinster Beobachtungswert
R = xmax – xmin
Beispiel Spannweite:
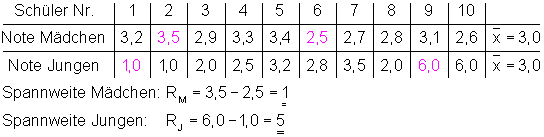
Die Spannweite bei den Mädchen ist also viel kleiner als bei den Jungen.
Dazu kannst du dir das 📽️Video Spannweite ansehen.
Der Quartilsabstand
Es kann allerdings auch vorkommen, dass nur ein Wert die Spannweite erhöht. Z. B. hat Spieler 9 wesentlich mehr Punkte in einem Videospiel erlangt als alle anderen.
| Spieler 1 | Spieler 2 | Spieler 3 | Spieler 4 | Spieler 5 | Spieler 6 | Spieler 7 | Spieler 8 | Spieler 9 |
|---|---|---|---|---|---|---|---|---|
| 102 | 102 | 105 | |107 | 109 | 111 | 114 | 118 | 867 |
Die Summe aller Werte beträgt also 1735, der Mittelwert = 192,77, der Median 109 und die Spannweite = 867 – 102 = 765.
Im letzten Beitrag haben wir bereits den Median kennengelernt. Er teilt einen nach Größe sortierten Datensatz in der Mitte. Anders ausgedrückt: links und rechts vom Median liegen gleich viele Beobachtungswerte.
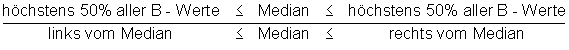
Definition Quartile
Danach kann man die linke und rechte Hälfte noch einmal unterteilen. Dadurch erhält man vier gleich große Bereiche. Die Grenzen zwischen diesen Bereichen nennt man Quartile. Das Wort quart ist lateinisch und bedeutet Viertel. Quartile teilen eine Datenreihe also in Viertel auf.
Beispiel:
Die Liste enthält die Körpergröße von 13 Schülern. Die Merkmalsausprägungen sind nach Größe geordnet. Um den Median zu finden, addiert man 1 zur Anzahl der Werte und dividiert dies durch 2. Da (13 + 1) / 2 = 8, liegt der Median bei der Merkmalsausprägung 1,70 m.
Um die 1. Quartile zu finden, addiert man 1 zur Anzahl der Werte und multipliziert mit 0,25. Also (13 + 1) *0,25 = 3,5 . Deshalb bilden wir den Durchschnitt aus dem 3. und 4. Wert. Wir erhalten also die Merkmalsausprägung 1,675.
Um die 3. Quartile zu finden, addiert man 1 zur Anzahl der Werte und multipliziert mit 0,75. Also (13 + 1) * 0,75 = 10,5. Deshalb bilden wir den Durchschnitt aus dem 10. und 11. Wert. Wir erhalten also die Merkmalsausprägung 1,775.
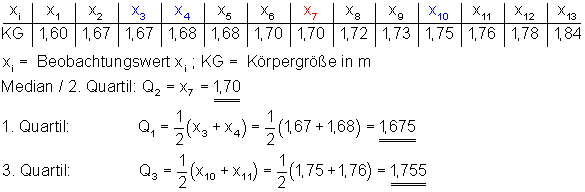
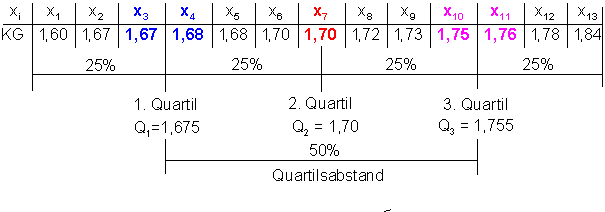
Quartile:
Wir haben dadurch alle Beobachtungswerte in 4 Viertel unterteilt:
Etwa 25% aller geordneten Beobachtungswerte sind deshalb kleiner als das 1. Quartil.
Ca. 50% aller geordneten Beobachtungswerte sind also kleiner als das 2. Quartil.
Etwa 75% aller geordneten Beobachtungswerte sind kleiner als das 3. Quartil.
Zwischen dem 1. und 3. Quartilliegen liegen folglich 50% aller Beobachtungswerte. Dieser Bereich wird auch Quartilsabstand genannt. Dadurch haben wir ein Maß dafür, wie weit die meisten Werte voneinander entfernt sind.
Definition Quartilsabstand
Der mittlere 50%-Bereich aller Beobachtungswerte heißt Quartilsabstand. Man berechnet ihn folgendermaßen:
QA = Q3 – Q1 Also 3. Quartile minus 1. Quartile
In diesem Beispiel beträgt der Quartilsabstand also 1,755 m – 1,675 m = 0,08 m
Das bedeutet, 50% der Daten liegen in dem Bereich der Bandbreite von 8 cm. Das heißt, etwa 50% der Körpergrößen liegen zwischen 1,675 m und 1,755 m. Mit anderen Worten: die meisten Beobachtungswerte liegen nur 8 cm auseinander.
Vergleich zwischen Quartilsabstand und Spannweite
Wir haben jetzt also zwei Methoden, um zu messen, wie weit die Beobachtungswerte voneinander entfernt sind. Beide ergänzen sich dabei:
| Quartilsabstand | Spannweite |
| Von Ausreißern unabhängig. Gibt die Breite des mittleren Bereichs an, in dem ca. 50% aller Werte liegen. |
Vom kleinsten und größten Wert abhängig. Gibt die Gesamtbreite an in dem alle Werte liegen. |
Beispiel:
Ein Landwirt misst im Monat April jeweils mittags um 12 Uhr die Außentemperatur und trägt sie dann in eine Tabelle ein.
Berechne danach den Mittelwert, die Spannweite und den Median! Berechne anschließend das 1. und 3. Quartil und den Quartilsabstand!
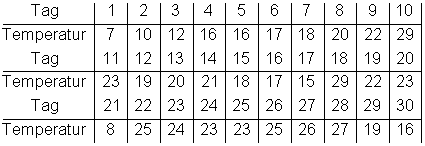
Wir berechnen den Mittelwert. Danach ordnen wir die Daten in einem Stängel-Blatt-Diagramm. Dabei ordnet man die Daten erst nach den Zehnerzahlen (Stängeln). Danach schreibt man die Einerzahlen (Blätter) der Größe nach hinzu.
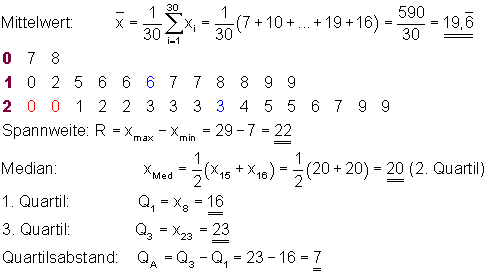
Definition Boxplot
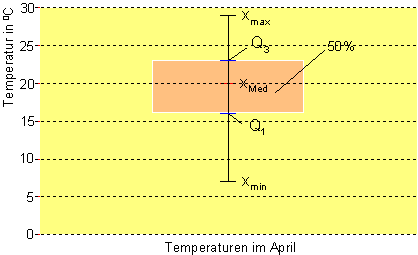
Das Wort Box ist englisch und bedeutet Kasten, plot bedeutet zeichnen. Ein Boxplot ist also eine Zeichnung mit einem Kasten. Darin zeichnet man den Median, den größten, kleinsten Wert und und die Quartile.
So kann man gut die Verteilungen vergleichen. Man sieht damit auf einen Blick, welche Spannweite die Werte haben und ob die Verteilung mehr nach links oder rechts abweicht.
Die Ergebnisse lassen sich in einem Boxplot-Diagramm darstellen:
Varianz und Standardabweichung
Wir betrachten noch mal die Notenverteilung von Mädchen und Jungen aus dem vorigen Beispiel.
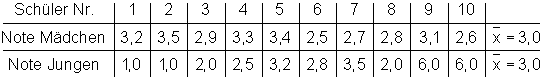
Der Mittelwert ist in beiden Fällen gleich, die Streuung um diesen ist unterschiedlich.
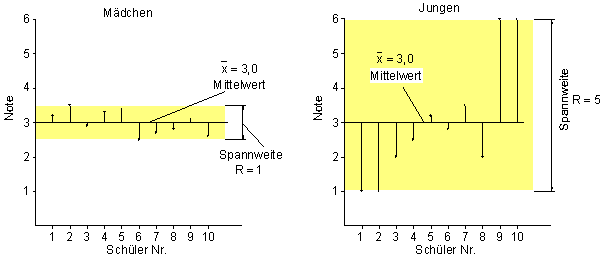
Es gibt eine weitere Methode, um die Abweichung zu messen:
Definition Varianz
Dazu kannst du dir das 📽️Video Standardabweichung und Varianz ansehen.
Die Abweichung eines Beobachtungswertes berechnet man aus der Differenz zum Mittelwert. Die Formel dazu lautet:
x_1 - \bar xEin Junge mit der Note 1 hat also die Abweichung 1 – 3 = -2. Ein Junge mit einer 6 die Abweichung 6 – 3 = 3.
Um die Abweichung aller Beobachtungswerte in einem Wert zu erhalten, müssten wir alle Abweichung addieren. Dabei würden sich die positiven und negativen Werte aufheben. Um das zu vermeiden, quadriert man jeden einzelnen Wert. Aus der Summe aller Werte bildet man dann den Mittelwert. Damit haben wir einen Wert für die Abweichung aller Beobachtungswerte. Dies nennt man Varianz.
Varianz Formel
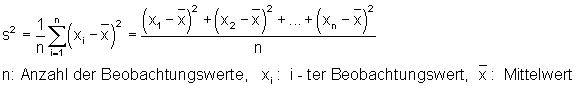
Beispiel für die Berechnung der Varianz einer Datenreihe
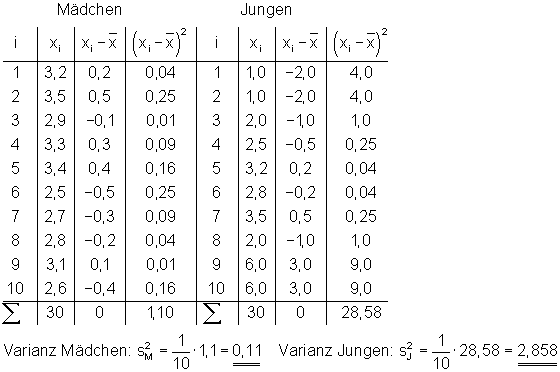
Die meisten Daten sind mit einer Einheit behaftet, z. B. Meter (m). Weil die Varianz eine Summe von Quadraten ist, hat sie als Einheit das Quadrat der Einheit, z. B. m2. Die Note 12 wäre ja toll, aber all die anderen…! 😉
Standardabweichung
Um wieder auf die ursprüngliche Einheit zu kommen, zieht man deshalb die Wurzel aus der Varianz. Dieser Wert wird Standardabweichung genannt.
Standardabweichung Formel
![]()
Am besten fertigt man wie oben gezeigt eine entsprechende Tabelle an. Dadurch hat man auch Kontrolle der Daten. Denn die Summe der Abweichungen muss Null ergeben.
Varianz bei einer Stichprobe:

Berechnung der Standardabweichung aus einer Häufigkeitstabelle
Im obigen Beispiel haben wir die Varianz und Standardabweichung einer Datenreihe berechnet. Dabei standen uns für jeden einzelnen Schüler die Noten zur Verfügung. Z. B. haben die Jungen 1. und 2. jeweils eine 1 geschrieben. Wenn wir die Daten in einer Häufigkeitstabelle haben, müssen wir jede Note mit deren Anzahl multiplizieren. Z. B. haben zwei Jungen eine 1 geschrieben. Dabei geht man ähnlich vor wie bei der Mittelwertbildung.
Hier noch einmal die Formeln zum Mittelwert:
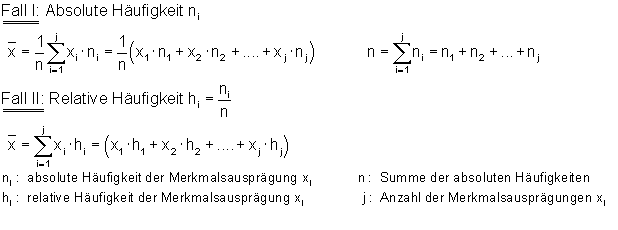
Wenn wir die Varianz einer Häufigkeitstabelle berechnen, müssen wir also auch erst die Abweichung jeder Note vom Mittelwert berechnen. Zweitens diese Werte jeweils quadrieren. Drittens all diese Werte addieren.
Absolute Häufigkeit bedeutet dabei, 5 Schüler haben eine 1 geschrieben. Relative Häufigkeit bedeutet, 5 von 50 Schülern, also 0,1 aller Schüler, haben eine 1 geschrieben.

Beispiel:
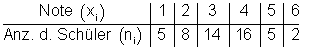
Erst einmal berechnen wir die Varianz und Standardabweichung aus der absoluten Häufigkeit der Gesamtzahl aller Schüler ni:
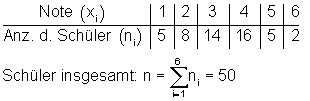
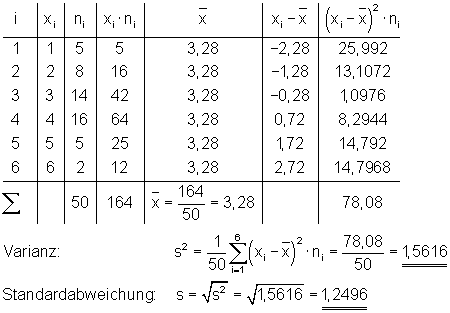
Beispiel:
Als nächstes berechnen wir dies aus der relativen Häufigkeit:
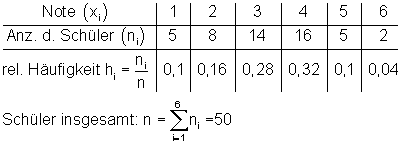
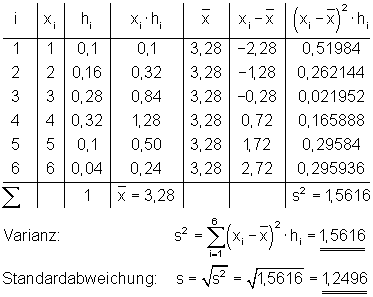
Du kannst dabei selber entscheiden, was dir lieber ist.
Berechnung der Standardabweichung aus einer klassierten Häufigkeitstabelle

Schauen wir uns z. B. diese Daten an, in denen die Körpergröße in Klassen eingeteilt sind. Wenn wir hier den Mittelwert bilden, müssen wir zuerst jede Klassenmitte mit deren Häufigkeit multiplizieren. Z. B. ist die Klassenmitte zwischen 160 cm und 170 cm 165 cm. Hier noch einmal die Formel für die Berechnung des Mittelwertes in einer klassierten Häufigkeitstabelle:
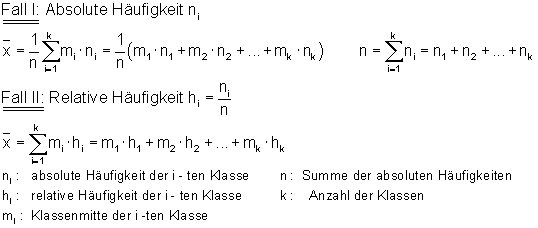
Wenn wir die Varianz einer klassierten Häufigkeitstabelle berechnen, gehen wir ähnlich vor.
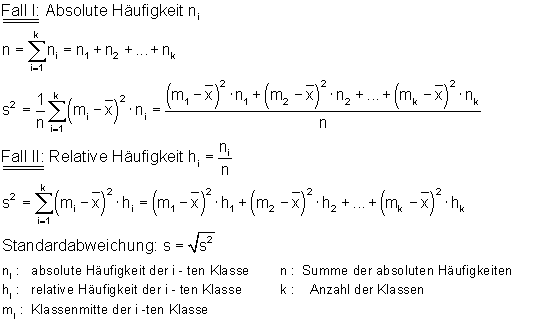
Beispiel:
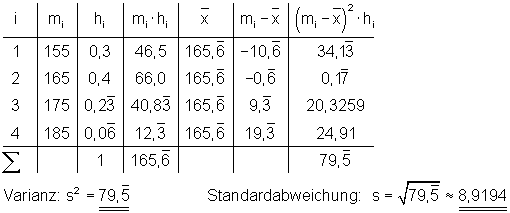
Jetzt kannst du einmal üben. Bestimme aus der klassierten Häufigkeitstabelle für die Körpergröße die Standardabweichung!
Hier die absolute Häufigkeit:

Hier die relative Häufigkeit:
Zusammenfassung:
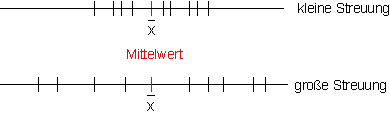
Die Standardabweichung ist ein Maß dafür, wie hoch die Aussagekraft des Mittelwertes ist.
Wenn die Standardabweichung klein ist, liegen alle Beobachtungswerte nahe am Mittelwert.
Wenn die Standardabweichung groß ist, liegen die Beobachtungswerte weit um den Mittelwert gestreut.
Somit haben wir alles Wichtige aus der Statistik behandelt. Im nächsten Beitrag fasse ich die wichtigsten Begriffe der Statistik noch einmal zusammen.
Alle Formeln zur beschreibenden Statistik sind hier übersichtlich zusammengestellt.
Schließlich findest du hier eine Übersicht über alle Beiträge zum Thema Statistik.

