Nachdem wir uns in den letzten beiden Beiträgen mit Steigung, Tangente. Differentialquotient und Ableitung beschäftigt haben, will ich die die Differentialrechnung noch einmal von einer anderen Seite erklären. Diesmal mit dem Schwerpunkt auf die Sekantensteigung. Zuerst zeige ich anhand eines Beispiels, dass die Steigung einer Geraden sich also auch mit dem Differenzenquotienten bestimmen lässt. Danach stelle ich die Formeln für die Sekantensteigung und Tangentensteigung vor. Zuletzt gehe ich auf den Zusammenhang zwischen Differenzenquotient, Differentialquotient, Ableitung und Steigungsfunktion ein.
- Steigungsformel für eine Gerade
- Sekantensteigung und Tangentensteigung
- Differenzenquotient, Ableitung und Steigungsfunktion
- Ableitungsbeispiel
- Extremstellen und Wendestellen
Die Steigung einer Geraden
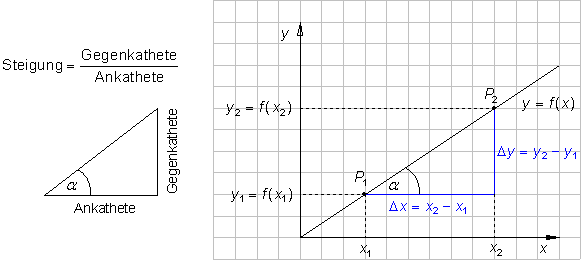
Steigungsformel für eine Gerade
Beispiel:
Mit zwei Punkten P0 (2 | 3) und P1 (5 | 7) kann man die Steigung der Geraden berechnen:

Δ Ist das mathematisches Zeichen für Differenz, deshalb können wir schreiben:
x\Delta x = x_1 - x_0 Wir stellen die Gleichung um: | + x_0
\Leftrightarrow \Delta x + x_0 = x_1
\underline{\underline{\Leftrightarrow x_1 = x_0 + \Delta x }}
Deshalb können wir auch schreiben: f(x_1) = f(x_0+\Delta x)
Damit sieht die Steigungsformel so aus:
\color{blue}{\dfrac{f(x_1)-f(x_0)}{x_1-x_0}} = \color{blue}{\dfrac{f(x_0+\Delta x)-f(x_0)}{\Delta x}} Das nennt man den Differenzenquotient.
Wir überprüfen die Gültigkeit dieser Formel mit obigem Beispiel.
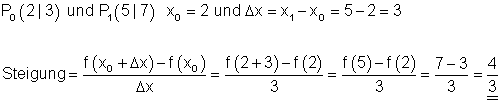
Die Steigung einer Geraden lässt sich also auch mit dem Differenzenquotienten bestimmen.
Dazu kannst du dir das 📽️ Video Differenzenquotient ansehen.
Sekantensteigung und Tangentensteigung
Die Steigung einer Geraden kann mal leicht berechnen, weil sie überall gleich ist. Bei ganzrationalen Funktionen ändert sich die Steigung jedoch.
Problem:
Wie groß ist die Steigung des Graphen einer beliebigen Funktion f(x) im Punkt P0? Wir können eine Gerade vom Punkt P0 zu einem Punkt P1 zeichnen. Diese Gerade nennt man Sekante. Die Sekantensteigung ist die mittlere Steigung zwischen den Punkten P0 und P1.

Was geschieht mit der Sekante, wenn wir den Punkt P1 immer weiter in Richtung P0 bewegen?
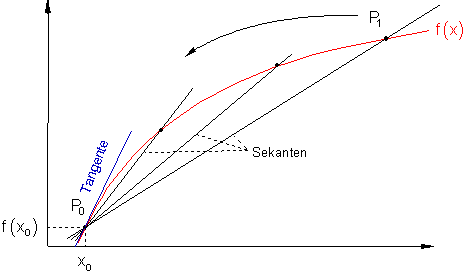
Die Sekante schmiegt sich immer mehr dem Graphen von f(x) an.
Wenn P1 auf P0 trifft, gibt es keine Sekante mehr. Sie ist dann zur Tangente geworden.
Die Tangente ist eine Gerade, die den Graphen von f(x) im Punkt P0 berührt. Per Definition ist die Steigung eines Graphen in einem Punkt P0 gleich der Steigung der Tangente an dem Graphen in diesem Punkt.
Dazu kannst du dir das 📽️ Video Sekante und Tangente ansehen.Differenzenquotient, Ableitung und Steigungsfunktion
Um die Steigung eines Graphen f(x) an der Stelle x0 also im Punkt P0 ( x0 | f(x0) ) zu berechnen, lässt man in der Formel für die Sekantensteigung das „delta x“ immer kleiner werden, was einer Verschiebung des Punktes P1 in Richtung P0 entspricht.
Die Sekantensteigung: \dfrac{f(x_1)-f(x_0)}{x_1-x_0} kann man auch mit dem Differenzenquotient berechnen: = \dfrac{f(x_0+\Delta x)-f(x_0)}{\Delta x} .
Dies bezieht sich auf eine konkrete Differenz zwischen zwei Punkten. Außerdem gibt es die durchschnittliche Steigung zwischen zwei Punkten an.
Die Steigung des Graphen von f(x) an der Stelle x 0 erhält man über die Grenzwertbildung
f '(x_0) = \lim \limits_{\Delta x\to 0} \dfrac {f(x_0 + \Delta x) - f(x_0)}{\Delta x}
Dies ist der Differentialquotient.
Grenzwertbildung bedeutet „delta x“ strebt gegen Null, wird also beliebig klein ohne exakt Null zu werden. Würde man für „delta x“ den Wert Null einsetzen, so entstünde ein undefinierter Ausdruck.
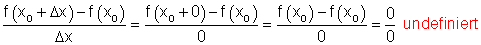
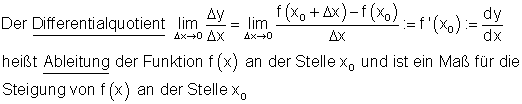
Dazu kannst du dir das 📽️ Video Differentialquotient-Differenzenquotient Unterschied ansehen.
Ableitungsbeispiel:

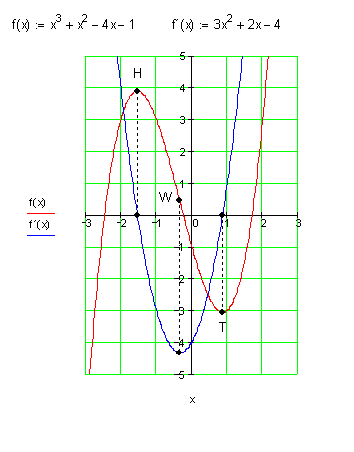
Statt Ableitungsfunktion f'(x) sagt man auch Steigungsfunktion, da diese Funktion für jeden Funktionswert x die Steigung der abgeleiteten Funktion an der Stelle x angibt.
Oben ist der Graph einer Funktion, sowie der ihrer Ableitungsfunktion in einem Koordinatensystem dargestellt.
Extremstellen und Wendestellen
An der Wendestelle (W) hat die Ableitungsfunktion einen Extremwert.
Dazu findest du hier Aufgaben zur Differentialrechnung II.
Und Aufgaben zur Differentialrechnung III.
Hier Aufgaben zur Differentialrechnung IV.
Und Aufgaben zur Differentialrechnung VI .
Im nächsten Beitrag werde ich die Differentiationsregeln erklären.
Hier findest du eine Übersicht über alle Beiträge zum Thema Differentialrechnung.


