Im letzten Beitrag habe ich die Symmetrie und Verlauf ganzrationaler Funktionen erklärt. Hier zeige ich, wie man die Nullstellen ganzrationaler Funktionen berechnet. Mit anderen Worten: Wir berechnen die Achsenschnittpunkte. Zuerst zeige ich Funktionen und deren Graphen mit einer, mehreren und keiner Nullstelle. Danach erkläre ich eine Regel für Nullstellen ganzrationaler Funktionen. Dann stelle ich einen interaktiven Rechner und einen Nullstellenfinder zur Verfügung. Anschließend stelle ich die Berechnungsverfahren vor: Faktorisierungsverfahren, Substitutionsverfahren, Polynomdivision, Horner- Schema. Dazu gibt es jeweils Videos. Am Schluß stehen Links zu Aufgaben.
-
- Schnittpunkt mit der y-Achse
- Schnittpunkt mit der x-Achse
- Beispiele für Achsenschnittpunkte mit Graphen
- Regel für Nullstellen ganzrationaler Funktionen
- Varianten von Polynomgleichungen
- Berechnungsverfahren für Nullstellen:
Faktorierungsverfahren mit Video - Substitutionsverfahren mit Video
- Polynomdivision
- Horner-Schema
- Links zu Aufgaben
Schnittpunkt mit der y-Achse
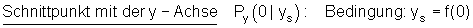
Zuerst schauen wir uns ein Beispiel an:
Beispiel:
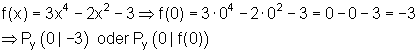
Die y-Koordinate von Py ist immer identisch mit dem Koeffizienten a0. Deshalb lässt sie sich aus der Funktionsgleichung ablesen.
Schnittpunkt mit der x-Achse
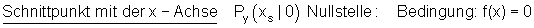
Von den quadratischen Funktionen (ganzrationale Funktionen 2. Grades) ist bekannt, dass sie zwei, eine oder keine Nullstelle haben können. Wie ist das jedoch bei ganzrationalen Funktionen höheren Grades?
Beispiele für Achsenschnittpunkte:
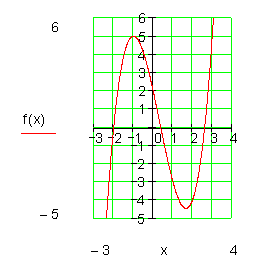
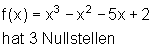
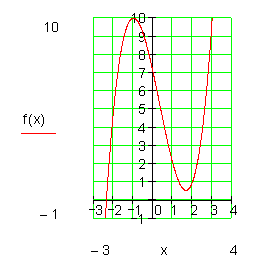
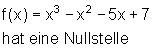
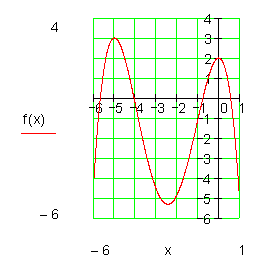
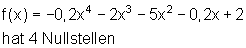
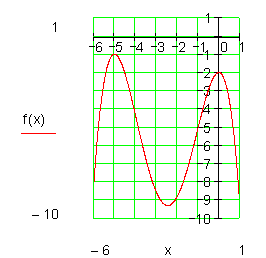
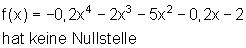
Regel für Nullstellen ganzrationaler Funktionen:
Eine ganzrationale Funktion n ten Grades hat höchstens n Nullstellen.
Wenn der Grad n ungerade ist, sie mindestens eine Nullstelle.
Rechner für ganzrationale Funktionen 4. Grades Interaktiv: Gib die Koeffizienten obiger Funktionen ein und verändere diese geringfügig. Beobachte dabei die Veränderungen am Graphen!
Rechner Nullstellenfinder Interaktiv:
Nachdem du einen Term eingegeben hast, errechnet das JavaScript die Nullstellen von Polynomen bis 9. Grades und zeichnet den Graphen.
Bevor man Verfahren zur Berechnung von Nullstellen ganzrationaler Funktionen behandelt, sollte man sich mit Polynomgleichungen zu beschäftigen, siehe auch hier. Man unterscheidet dabei mehrere Varianten von Polynomgleichungen, für die es unterschiedliche Lösungsverfahren gibt.
Varianten von Polynomgleichungen
Variante 1
In der Gleichung kommt nur eine einzige Potenz der Variablen x vor.
![]()
Falls n ungerade ist, darf der Radikand auch negativ sein. Dann gibt es genau eine Lösung der Wurzel. Dazu kannst du dir dieses 📽️ Video Polynomgleichung, 1 Potenz, Exponent ungerade, Radikand negativ ansehen.
Falls n gerade ist, darf der Radikand nur positiv sein. Dann gibt es zwei Lösungen. Dazu kannst du dir dieses 📽️ Video Polynomgleichung, 1 Potenz, Exponent gerade, Radikand positiv ansehen.
Variante 2
Die Polynomgleichung stellt eine quadratische Gleichung dar.
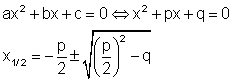
Diese lässt sich mithilfe der p-q-Formel berechnen, siehe auch hier.
Dazu kannst du dir die Videos 📽️p-q-Formel einfach erklärt (die Theorie) und 📽️quadratische Gleichung lösen mit p-q-Formel Aufgabe anschauen.
Variante 3:
Die Polynomgleichung stellt eine biquadratische Gleichung dar.
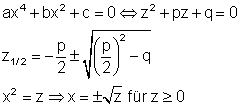
Die Substitutionsvariable z kann man mithilfe der p-q-Formel berechnen. Anschließend muss man zurücksubstituiert und die Wurzel ziehen. Dazu kannst du dir dieses 📽️ Video Polynomgleichung lösen, die eine biquadratische Gleichung ist ansehen.
Variante 4:
In der Polynomgleichung kommt kein absolutes Glied vor.
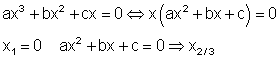
Die Variable x lässt sich ausklammern.
Dann berechnet man die Lösungen nach dem Satz vom Nullprodukt. Mit anderen Worten: Faktorisierungsverfahren. Das erkläre ich im nächsten Abschnitt.
Variante 5:
Die Polynomgleichung entspricht nicht einer der Varianten 1 bis 4.![]()
In vielen Fällen lässt sich die Lösung durch die Polynomdivision finden. Dazu muss aber eine Lösung bekannt sein.
Beispiele dazu mit allen Varianten: Polynomgleichungen.
Berechnungsverfahren für Nullstellen
Beispiel für das Faktorisierungsverfahren:
Das ist nur möglich, wenn kein absolutes Glied vorhanden ist, also keine Zahl alleine, sondern x in jedem Summanden vorkommt. Dann kann man x ausklammern. Wenn einer der beiden Faktoren 0 ist, haben wir schon eine Nullstelle, nämlich 0. Der Ausdruck in der Klammer ist eine quadratische Gleichung, die wir mit der p-q-Formel lösen können.

Dazu kannst du dir das 📽️ Video Faktorierungsverfahren ansehen.
Beispiel für das Substitutionsverfahren:
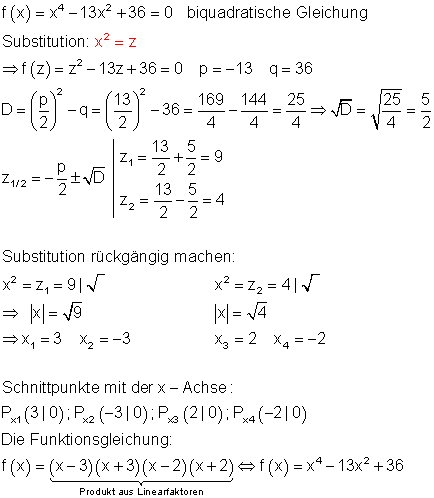
Dazu kannst du dir dieses 📽️ Video Polynomgleichung lösen, die eine biquadratische Gleichung ist ansehen.
Polynomdivision:
Ist eine Nullstelle einer ganzrationalen Funktion (Polynom) bekannt, dann kann der Grad des Polynoms durch Polynomdivision um eins verringert werden. Wenn das auf eine quadratische Gleichung führt, ist es ein leichtes, die weiteren Nullstellen zu finden. Folgendes Beispiel verdeutlicht das Verfahren der Polynomdivision:
Dazu kannst du dir das 📽️Video Polynomdivision ansehen.
Beispiel:

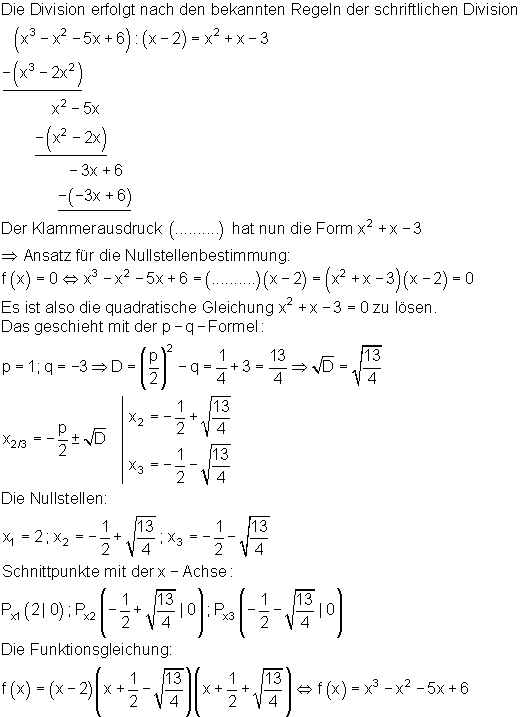
Horner-Schema:
Statt über die Polynomdivision kann der Grad einer ganzrationalen Funktion auch durch Anwendung des Horner- Schemas verringert werden.
Dazu kannst du dir das Video 📽️ Video Horner-Schema: Funktionswerte berechnen ansehen.
Wir betrachten wieder die Funktion:

Für die Berechnung weiterer Nullstellen von f (x) sind die Nullstellen des Restpolynoms zu bestimmen. Das geschieht durch Lösung der entsprechenden quadratischen Gleichung. Ergebnis siehe Beispiel mit Polynomdivision.
Beispiel:
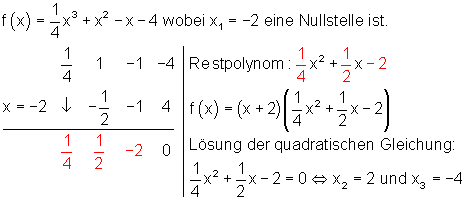
Beispiel:
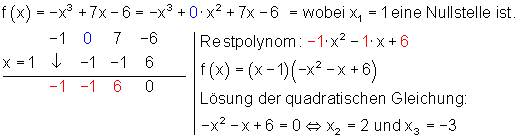
Wie die Beispiele zeigen, ist die Bestimmung des Restpolynoms mit dem Horner- Schema einfacher als mit der Polynomdivision.
Alle oben gezeigten Verfahren führen auf die Lösung einer quadratischen Gleichung. Falls dieses nicht gelingt, so werden numerische Verfahren benötigt, die an dieser Stelle nicht behandelt werden.
Dazu findest du hier 20 Aufgaben zur Polynomdivision und zum Bestimmen der Nullstellen, Schnittpunkte und Linearfaktoren. Außerdem gibt es praktische Tipps und Beispielen.
Und hier Aufgaben Achsenschnittpunkte und Graphen ganzrationaler Funktionen I
Außerdem findest du eine Übersicht über alle Beiträge zum Thema weitere ganzrationale Funktionen, darin auch Link zu weiteren Aufgaben.


