Hier findest du eine umfangreiche Formelsammlung der Analysis: Von den binomischen Formeln, Potenzgesetzen, Logartithmusgesetzen, p-q-Formel, quadratische Funktionen bis zur Integralrechnung, mit vielen Beispielen.
Binomische Formeln
| Binomische Formeln | Beispiel |
| (a + b)2 = a2 + 2ab + b2 |  |
| (a – b)2 = a2 – 2ab + b2 |  |
| (a + b)(a – b) = a2 – b2 | (2x +1)(2x – 1) = 4x2 – 1 |
Hier findest du weitere Beispiele dazu.
Potenzgesetze
| Potenzgesetz | Beispiele |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
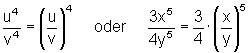| a0 = 1 |  |
 |
 |
Dazu findest du hier weitere Beispiele.
Logarithmengesetze zur Basis e
| Logarithmengesetz | Beispiel |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| e0 = 1 |  |
| ln(1) = 0 |  |
| ln(e) = 1 |  |
Hier findest du weitere Beispiele dazu.
p-q-Formel
 |
 |
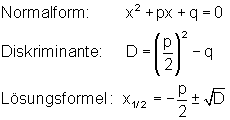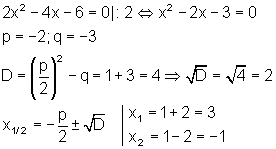Dazu gibt es hier weitere Beispiele.
Steigung einer Geraden durch zwei Punkte
 |
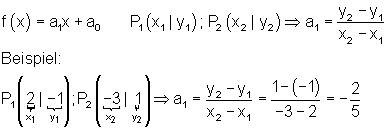Dazu findest du hier weitere Beispiele.
Orthogonale Geraden
Für die Steigung zweier senkrecht aufeinander stehender Geraden g und h gilt: |
Hier gibt es weitere Beispiele dazu.
Quadratische Funktionen
 |
Dazu findest du hier weitere Beispiele.
Tangente und Normale
Tangente und Normale an den Graphen von f(x) durch den Punkt P(x_0 | f(x_0))
Gleichung der Tangente: t(x) = f'(x_0)(x-x_o) + f(x_0) .
Dabei bildet f'(x_0) die Steigung.
Gleichung der Normalen: n(x) = -\frac{1}{f'(x)} (x-x_o) + f(x_0) ; f'(x_0) ≠ 0
Dabei bildet \frac{1}{f'(x)} die Steigung.
Beispiel: f(x) = -x^4 + 2x^3 \Rightarrow f'(x) = -4x^3 + 6x^2
P(1 | 1) \Rightarrow x_0 = 1 und f(x_0) = f(1) sowie f'(x_0) = f'(1) = 2
Die Tangente ist dann: t(x) = 2(x - 1) + 1 = \underline{\underline{ 2x - 1}} .
Die Normale ist dann: n(x) = -\frac{1}{2}(x - 1) + 1 = \underline{\underline{ -\frac{1}{2}x + \frac{3}{2}}}
Hier findest du weitere Beispiele dazu.
Funktion, Ableitung, Stammfunktion
| Funktion | Ableitung | Stammfunktion |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Regeln zur Differenzialrechnung
| Produktregel |  |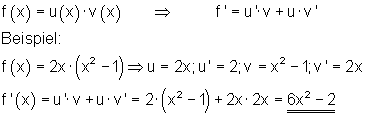
| Quotientenregel |  |
| Kettenregel |  |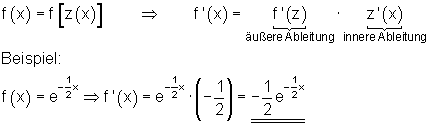
Integration durch Substitution
 |
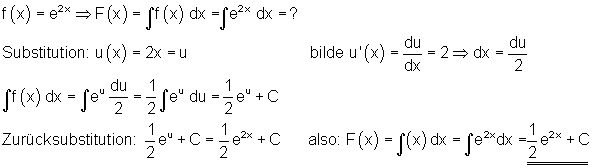Hier findest du weitere Beispiele dazu.
Partielle Integration
 |
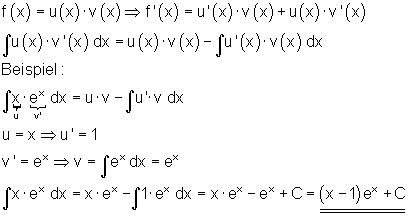Dazu gibt es hier weitere Beispiele.
Hier findest du eine Übersicht über weitere Beiträge zur Fortgeschrittenen Differential- und Integralrechnung, darin auch Links zu weiteren Aufgaben.
Dazu kannst du dir auch den Wikipedia-Artikel zur Analysis durchlesen.
